对比 B+ Tree 文件组织 / LSM Tree 文件组织(第一篇:B+ Tree)
B+ Tree 与 LSM Tree 是现今各类数据库中使用的比较多的两种数据结构,它们都可以作为数据库的文件组织形式,用于以相对高效的形式来执行数据库的读写。
本文简述了这两种数据结构的操作方式与操作开销,并对比了其自身的优缺点。
B+ Tree
B+ Tree 是我们比较熟悉的一种数据结构,它以节点(node)为单位来存储数据,每个 node 都可以存放多个 k-v 键值对,多个 node 以类似一棵树的形式组成完整的 B+ Tree,node 与 node 之间由指针来连接。
首先我们应当知道的是:B+ Tree 中保存的数据是有序的,我们通过 B+ Tree,可以实施查询、顺序访问、插入、删除的操作。
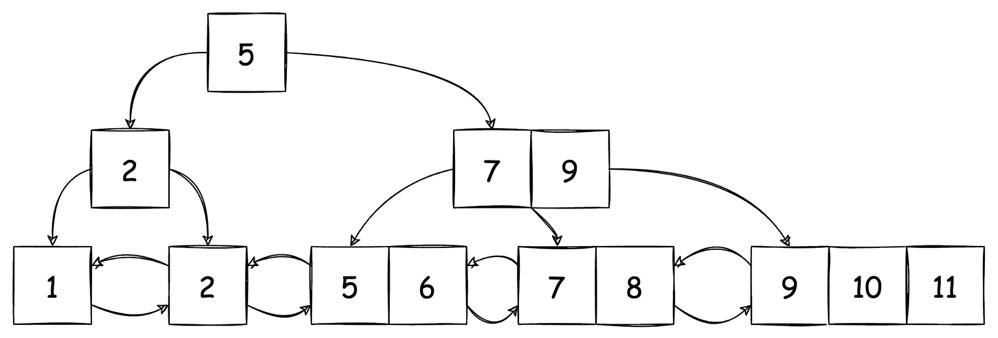
下图所示的就是一颗 B+ Tree (只保留 key,省略了具体的 value 值,下同):
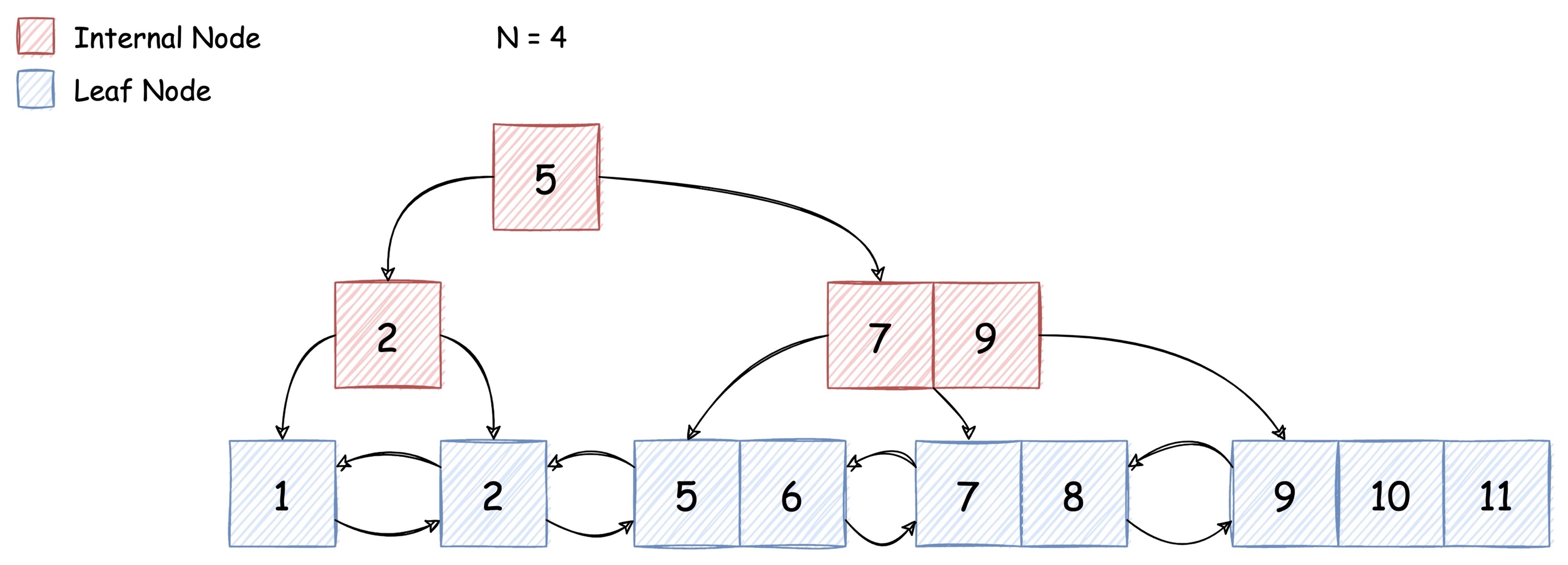
对于上图,我们有如下解释:
关于 node:
node 中的 key 保持有序,从左至右依次增加。node 之间的 key 也保持有序,左边 node 的 key 小于右边 node
红色 node 代表 internal node,即内部节点。internal node 包含的 k-v 键值对中,value 是指向下一个 node 的指针。在每一个 internal node 的最左边,还有一个指针,指向所有 key 都比本节点中最小 key 还要小的子节点。而 key 右边指针指向的子节点,其最小的 key 一定大于等于当前 key。
蓝色 node 代表 leaf node,即叶子节点。leaf node 包含的 k-v 键值对中,根据具体实现的不同 value 可能代表存放实际数据的文件的偏移量,也可能直接就是实际数据(clustering index)。另外我们会发现,leaf node 本身还是一个双向链表,他们包含了前后指针。
B+Tree 是完全平衡的,即所有的 leaf node 都处于同一层级
图上部的
N=4代表了这一棵 B+ Tree 的度(degree)是 4(也称 N-way B+ Tree)。- degree 的意思是,这棵树中任意一个 internal
node,它最多能指向多少个子节点,由于 internal node
最左边还有一个指针,因此一个 internal node 中最多只能包含
N-1个 key - node 中不仅限制了最大 key 数量,同时也限制了最少的 key 应大于
N/2 - 1。即每个 node 都至少是 “半满” 的 - 假如由于插入、删除等操作导致 node 中 key 的数量不满足要求,则必须对 node 进行 分裂(insert) 合并(delete)
- root node 既可以是 leaf,也可以是 internal。root node 的节点数不受 N 的限制
- degree 的意思是,这棵树中任意一个 internal
node,它最多能指向多少个子节点,由于 internal node
最左边还有一个指针,因此一个 internal node 中最多只能包含
B+Tree 的操作
一切对 B+ Tree 的操作,无论如何都需要在操作完成后仍然满足 B+ Tree 的定义要求。
Search
由于 B+ Tree 的有序性,search 操作非常简单,只要从 root 开始,根据需要查询的 key 来比较大小,一层层查找,直到找到 leaf node,之后在 leaf node 中按序找到对应的 k-v pair。
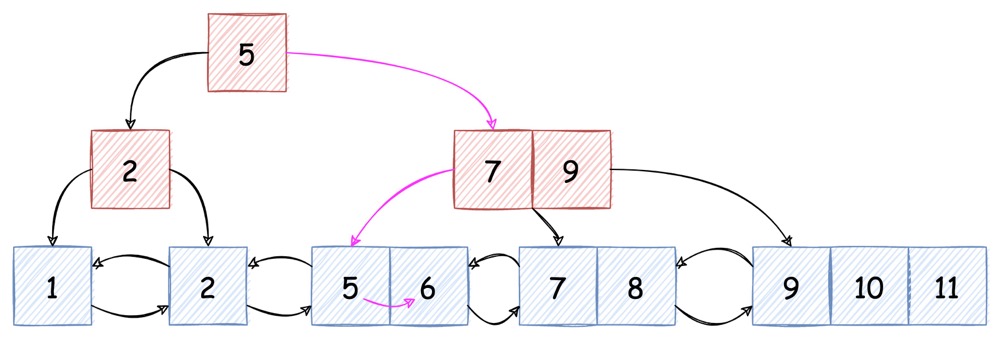
如上图紫色箭头所示的查找路径,我们期望找到 key == 6
的值,那么需要:
6 > 5 (root_key),进入右边 pointer 指向的子节点6 < 7 (far left of internal node),进入中间层 internal node 最左边 pointer 指向的子节点- 当前子节点已经是 leaf node,进入其中,依次对比,最终找到
k == 6的节点
我们发现,对于一颗高为 h 的 B+ Tree,最多只需要
(h - 1) + (N - 1) 次对比,就能找到(或确定不存在)值。
其中,
h - 1代表了查找 node 的次数,由于实际中磁盘存储的单位即是 node,因此h - 1可以看做是I/O次数N - 1代表了在 node 内部查找,由于实际中 node 都会被读入内存,因此 node 内的查找开销几乎可以忽略不计
Sequential Access
由于 leaf node 中包含了指向下一个 leaf node 的指针,因此对于类似
select * from tbl where i > 5这样的
顺序访问,只要找到第一个满足条件的 leaf node 后,就可以直接通过 next
指针来定位下一个 node。
假如是 clustering index (聚集索引)的实现,由于 node
之间的有序性,最佳情况下其数据在磁盘中的实际存储位置也是顺序存储的,那么顺序访问就会非常高效。
当然,如果 leaf node 只是指向了文件 offset,那么对 leaf node 的顺序访问并不代表对文件的顺序访问,这种情况下我们可以将范围内的 leaf node 按 offset 重排序之后再访问,因为多数查询并不要求结果集有序(“无序是关系模型之美” -- Andy Pavlo 如是说),这样就能顺序访问文件了。
Insertion
插入动作是一个多步判断的过程:
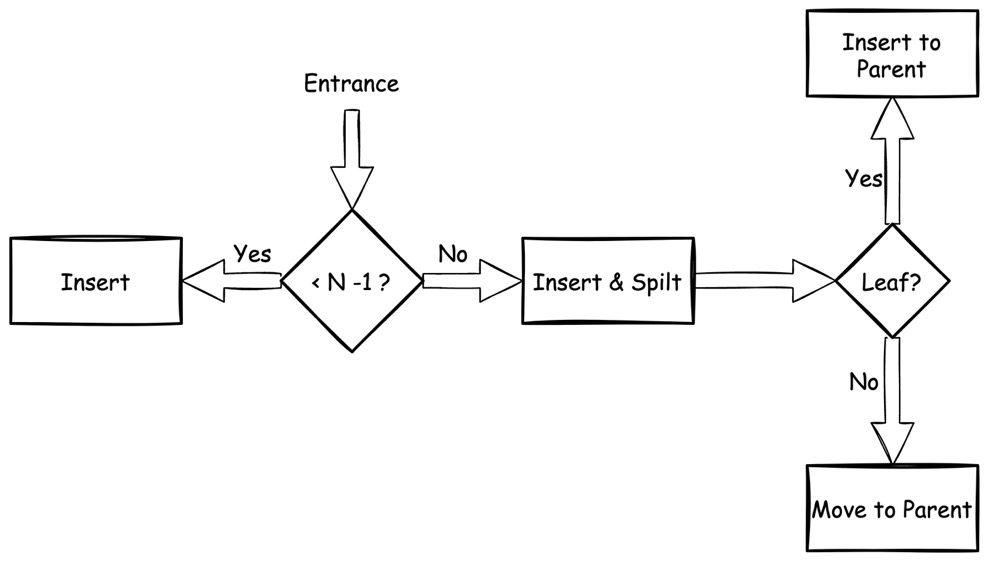
无论插入的是 internal 还是 leaf node,只要 node 中包含的 key 数量没有超过
N-1,那么就可以简单的将其插入:
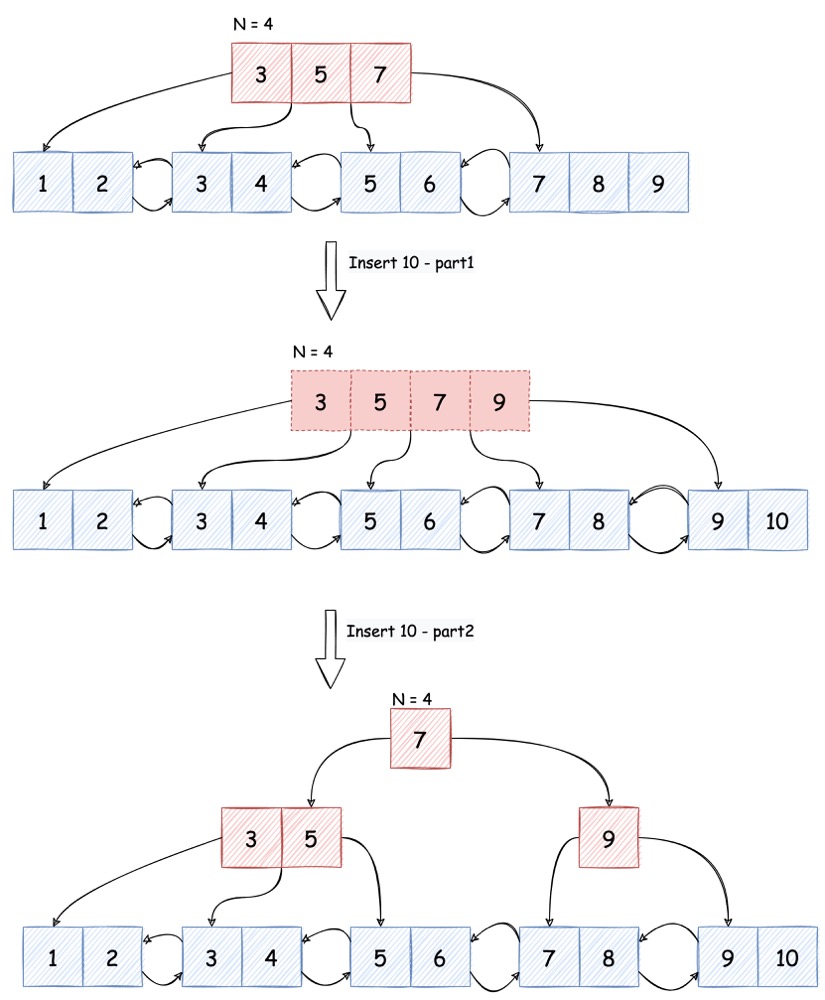
一旦插入的 node 已满,这个时候就需要先将 key 插入,之后将 node 从中间一分为二,且:
假如 node 本身是 leaf node,则将分裂出新节点的最左 key 作为新值,插入他们的 parent node

假如 node 本身是 internal node,则将分裂出新节点的最左 key 移除,插入他们的 parent node
Deletion
删除动作,同样也是多步判断:
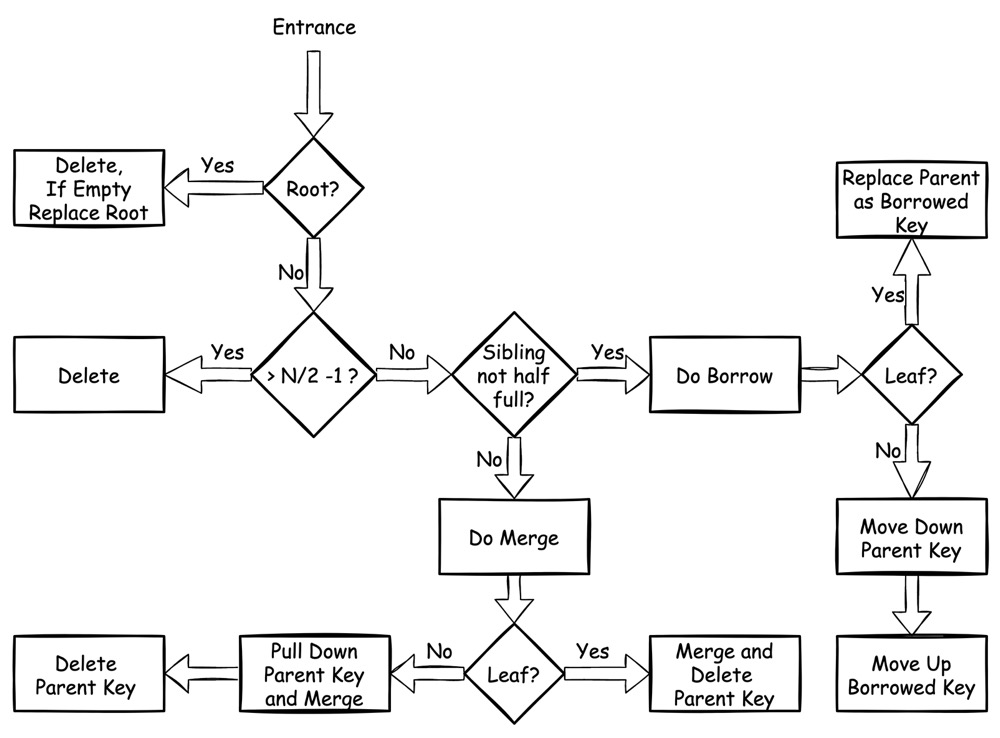
假如删除的是 root node,可以不受限制直接删除,如果 root node 为空则需要将下层 node 提升为 root
假如删除的 node 中 key 的数量
> N/2 - 1,那么可以直接执行删除后结束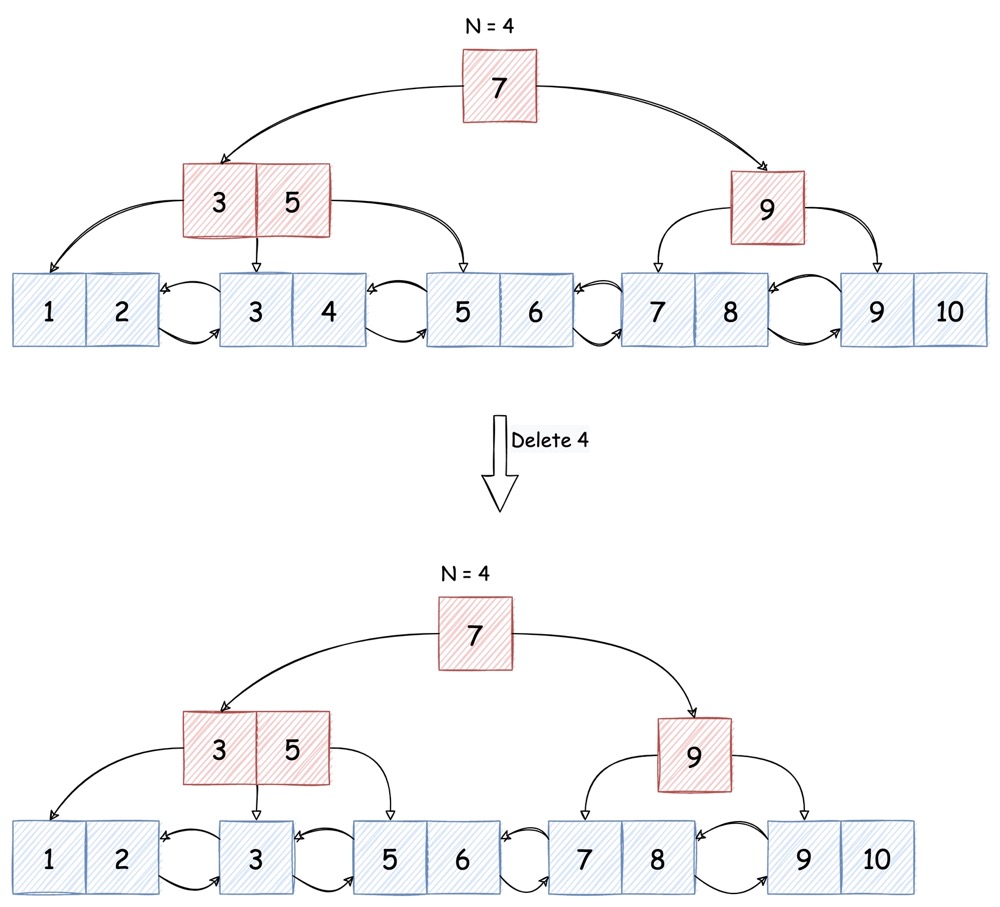
一旦删除的 node 只有半满(half full),就必须执行如下操作:
若其左右 sibling(同属一个 parent 下的兄弟)中有任意一个不是半满,就可以将其内的 key “借调” 到当前 node
Leaf:
借左 sibling:将左 sibling 的最后一个 key 迁移至当前 node,更新 parent node 中指向当前 node 的 key 替换为借调来的新 key

借右 sibling:将右 sibling 的第一个 key 迁移至当前 node,更新 parent node 中指向当前 node 的 key 为借调来的新 key,并将 parent node 中指向右 sibling 的 key 替换为右 sibling 新的最左侧 key

Internal:
借左 sibling:
- 将左 sibling 的最后一个 key 迁出,上移替换 parent 中指向当前 node 的 key
- 将 parent 中被替换的 key 下移,与当前最左侧 pointer 合并,添加至当前节点,并更新该 pointer 指向的所有 children node 的 parent。将左 sibling 的最后一个 key 包含的 pointer 作为当前节点的新最左侧 pointer
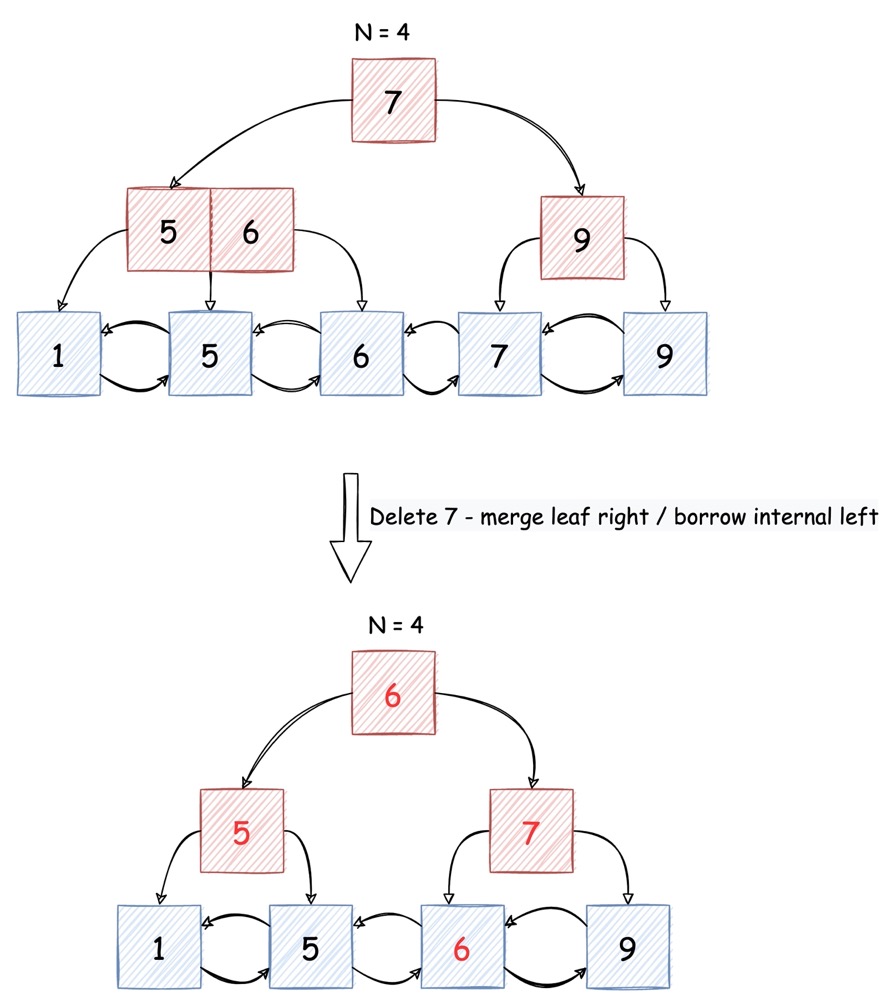
借右 sibling:
- 将右 sibling 的第一个 key 迁出,将该 key 对应的 pointer 作为右 sibling 的新最左侧 pointer,原来的最左侧 pointer 暂存。上移替换 parent 中指向右 sibling node 的 key
- 将 parent node 中被替换的 key 下移至当前节点尾部,对应的 pointer 为上一步暂存的 pointer,更新该 pointer 指向的 children node 的 parent
若无 sibling 可借,则必须和左侧或右侧的 sibling 合并:
Leaf:
- 向左合并:直接并入左 sibling,更新链表指针,删除 parent 中指向当前 node 的 key
- 向右合并:直接并入右 sibling,更新链表指针,删除 parent 中指向当前 node 的 key
Internal:
- 向左合并:将 parent 中指向当前 node 的 key 下移,删除其对应的 pointer,与当前 node 剩余 key 合并至左 sibling,更新当前 node children 的 parent
- 向右合并:将 parent 中指向右 sibling 的 key 下移,删除其对应的 pointer,与当前 node 剩余 key 合并至右 sibling,更新当前 node children 的 parent

B+ Tree 结合 Buffer Pool 优化性能
基于前文的描述,我们会发现,B+ Tree
最大的优势,如同其他平衡树一样,就是增删查改的时间复杂度都是O(logn)
,这很优秀。
我们需要进一步考虑的是,为什么要用 B+ Tree,而不是其他的类似红黑树(甚至是跳表)之类的数据结构呢?根源主要还是在于存储介质。
优化 B+ Tree 的速度
磁盘相对来讲还是太慢了。假如数据都仅仅存储在内存中,那么哈希表、树、跳表等结构都完全可以,因为读写数据所花费的时间(相对于磁盘而言)非常快。而在面向磁盘(disk-oriented)的数据库设计中,I/O 开销是需要重点考虑的部分。

根据上图(来源)的数据,mem 的速度可以达到 disk(hdd)的上万倍。

在根据上图(来源)从更细分的 sequential 和 random 的角度看,sequential 下 mem 的速度只比 disk 快 10 倍以内,而 random 下差距瞬间扩大到 10 万倍!
鉴于通常我们都无法将数据库中的数据完整的放在 mem 中,因此针对磁盘 I/O 特性而对存储结构进行优化是必须的,通常我们可以想到如下几种方法:
- 缓存层:最容易想到,使用效果通常也最立竿见影。其本质思想就是将热点数据缓存在内存中,以提高访问速度
- 尽量使用sequential I/O:鉴于 sequential 与 random 巨大的速度差异,我们当然期望尽可能多的将读写都以 sequential I/O 的形式来实施
- 尽量减少 I/O 次数:每执行一次 I/O 除了操作磁盘本身的开销外,系统调用相关的开销也很可观,因此用 10 次 I/O 每次读取 1 byte 和 1 次 I/O 读取 10 bytes 相比一定慢得多
与操作系统一样,数据库对磁盘数据的管理也是以 Page
为单位的,一个 Page 的容量从 4kb ~ 64kb 不等,在 B+ Tree
的实现中通常一一个 Page 用以代表一个 node,由于
Page 容量较大,因此大多数情况下 insert 和 delete
都不会涉及到 split 或 merge。同样的,由于 spilt 和 merge 较少发生,整个
B+ Tree 的层数也就相对较低。
再考虑 B+ Tree 的查找过程,我们会发现从 root 开始逐层向下搜索,每下一层都会读取一个不同的 node,产生一次 I/O,我们无法保证不同 node 能紧凑的存放,因此这种 I/O 是 random I/O。
基于此,层数越低,I/O 次数越少。
还记得 leaf node 之间存在前后指针,在理想情况下,leaf node 间的范围读取,可以全部以 sequential 的方式进行,而不需要再通过树来搜索。但随着 B+ Tree 中数据的不断变化,leaf node 之间将逐渐失去顺序的特性,产生碎片,这会导致 sequential I/O 逐渐退化为 random I/O,因此需要做碎片整理。
同样的,如果按主键序插入,则都是顺序 I/O(无论是否是 clusterring index),插入效率就会很高(UUID 做主键的另一个弊端)。
最后,为了尽可能的减少不必要的 disk 访问,引入 Buffer Pool
来做缓存层,代理所有的 disk 访问请求。由于 B+ Tree 的 internal node
只存放 key 和 pointer,占用空间非常小,所以一个 Page
中能存放大量 key-pointer pair,这也让 Buffer Pool 中存放下所有的
internal node 成为可能。
假设 Buffer Pool 中存放了所有 internal node,那么每一次点查(point search)最多只需要一次 random I/O。
Buffer Pool
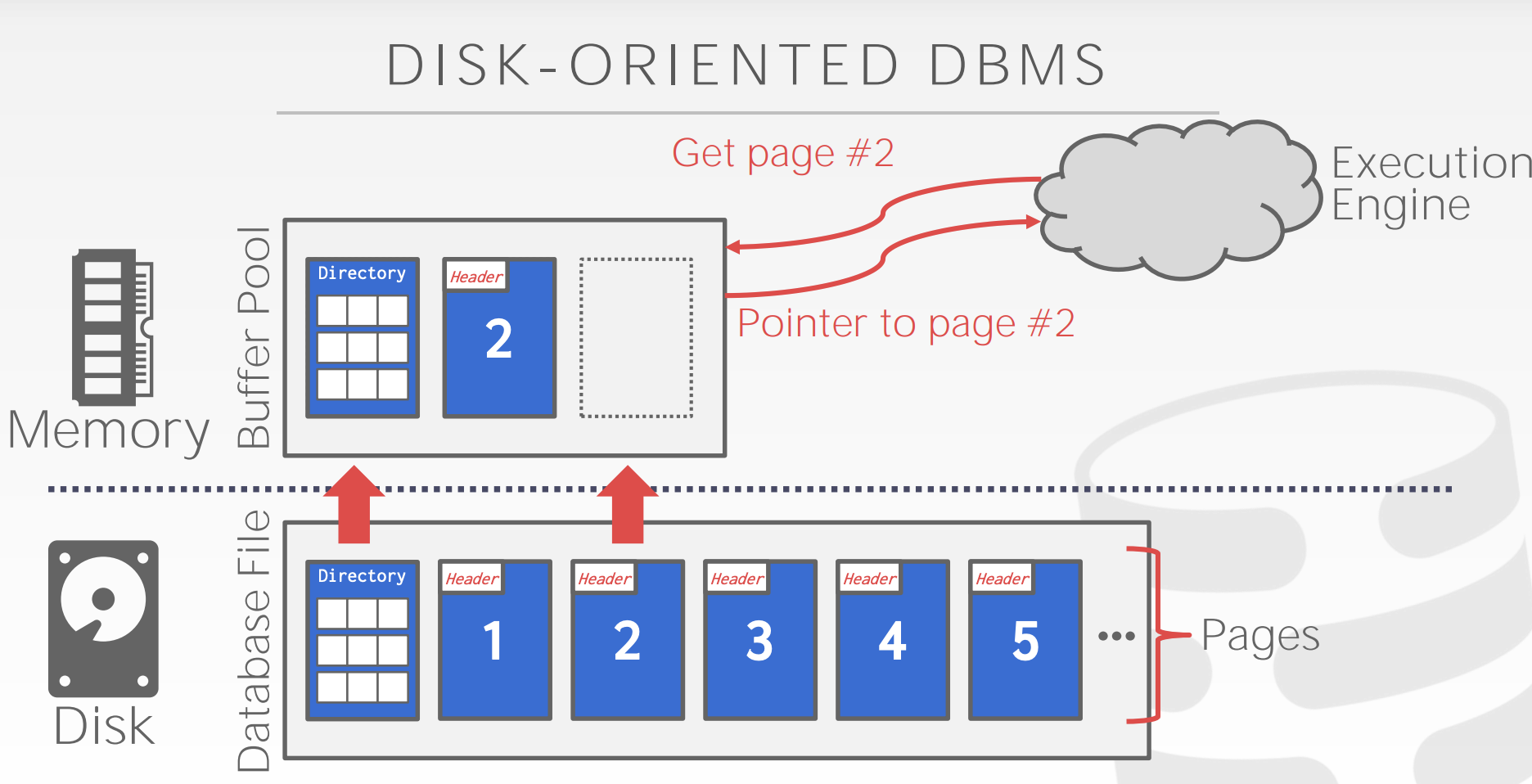
如上图(来源)所示,Buffer Pool 正好处于 disk 和 mem 之间,负责代理上层应用对 disk 数据的读写。其下层的 DiskManager 可以作为 Buffer Pool 的一个组件,而 B+ Tree 位于上层的 Access Method 中,因此 B+ Tree 的操作与 Buffer Pool 并不属于同一个层级。(如下图)

Buffer Pool 的应用,能够为数据库读写带来如下改善:
- READ:能够极大的降低 read I/O。对于需要被反复访问的热点数据,良好的算法与合理的 Buffer Pool 容量可以使其尽可能地待在内存中,以降低 disk I/O,理想情况下,甚至可以完全避免访问磁盘。
- WRITE:与 read 不同,持久化要求 write 操作迟早要落盘,因此 Buffer Pool 能做的更多的是延缓 write 而不能像消除 read I/O 一样消除 write I/O。但正因为延缓了 write,这能让随机的 write 操作被尽量的集中、合并。对同一块数据的多次写入可以仅在内存中完成,最后再刷盘。不同随机块的数据也许在一段时间后满足了顺序写入的要求,可以一次写入完成。
Buffer Pool 可以由如下几个组件构成:
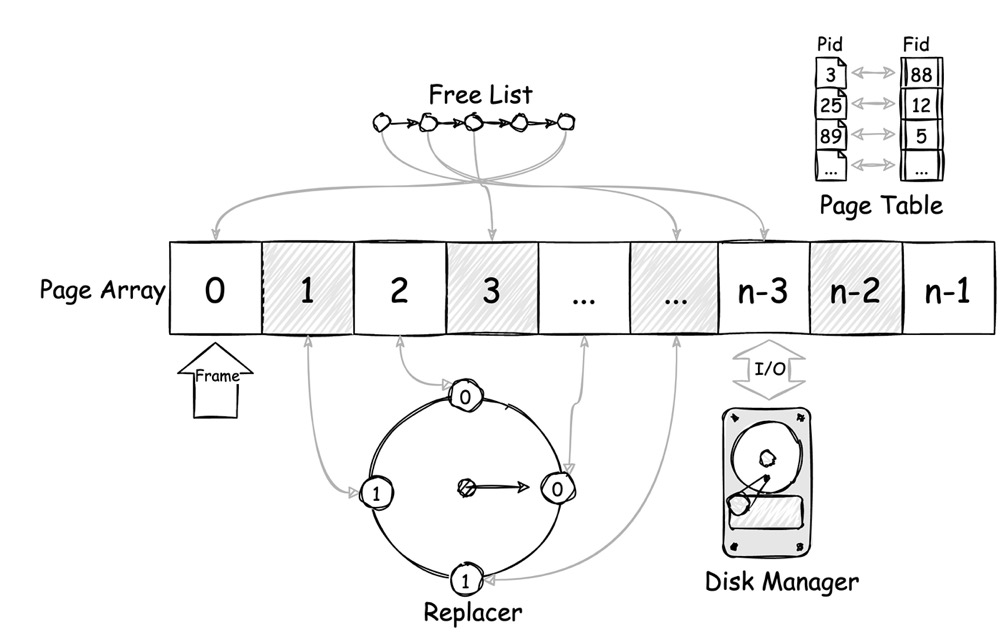
- Page Array:Buffer Pool 的主体,是一大块以
Page为操作单位(称为 Frame)的内存,用于存放数据 - Free List:用于管理 Page Array 中空闲 Frame 的线性表,期望从 Page Array 中申请 Frame 时优先从 Free List 中获取
- Page Table:Page id 与 Page Array 中 index(称为 frame id)的映射关系,用于通过 Page id 快速查找数据
- Disk Manager:和 disk 交互,进行磁盘读写,它可以持有一些 I/O 线程来专门负责 I/O 操作
- Replacer:当 Page Array full 的时候需要将一些数据换出,以便于换入新数据。替换算法通常有 LRU、Clock 等
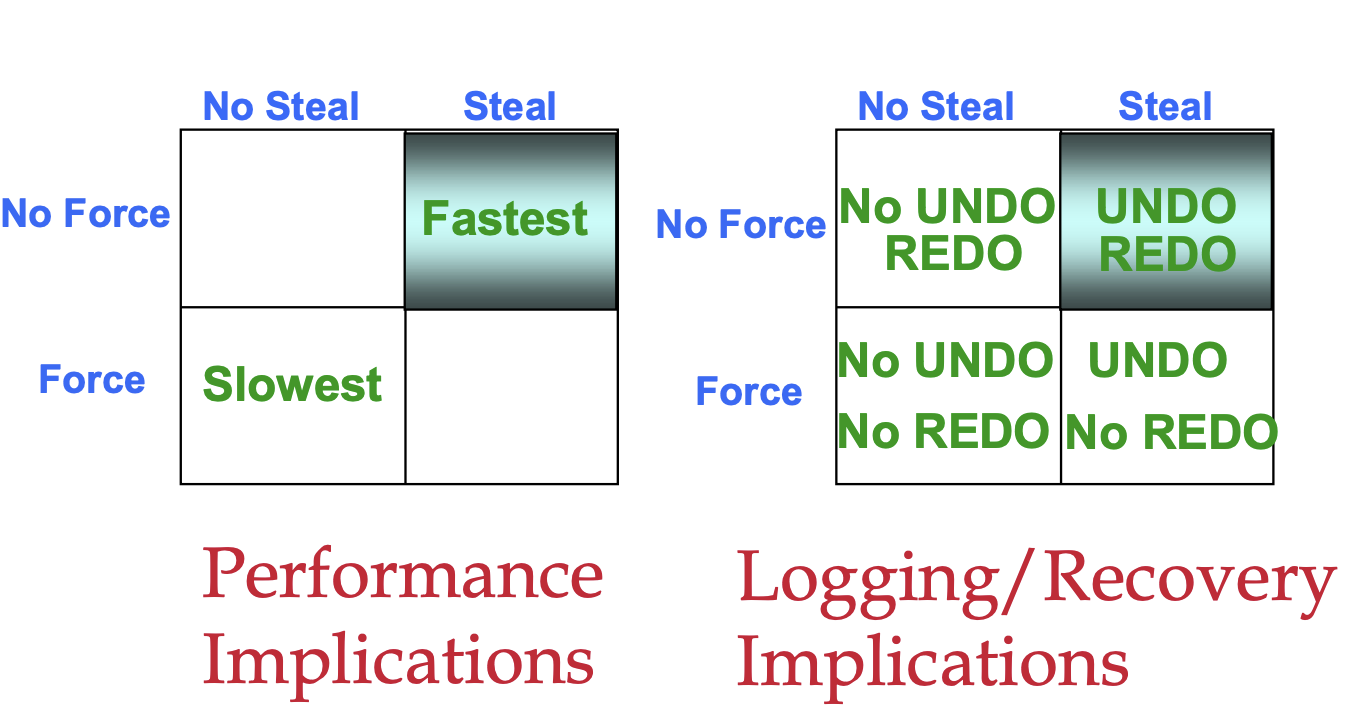
有趣的是,在事务型数据库中,为了保证 ACID 事务的 A 和 D,对 Buffer Pool 刷写数据和替换策略的设计上,有如下几种实现方式:
- 换入换出:
- No Steal: 某个事务中对 Page 的 uncommitted 修改,在 commit 之前都仅保持在 mem 中,而绝不落盘
- Steal:在事务执行过程中,Page 可以随时被换出并落盘
- 刷写数据:
- Force:在某个事务提交时,所有事务中修改的数据都应全部落盘
- No Force:事务提交后,其修改也可能还未落盘
为了保证 AD,最简单的实现方式就是 No Steal + Force:未提交的事务在 crash 后一定会丢失(因为未落盘),已提交的事务在 crash 后一定会存在(提交时同步落盘)。
但性能会大受影响:
- 由于未提交事务中的 Page 不能被换出,则 Buffer Pool 中需要持有所有当前正在执行事务的 Page,导致同时执行的事务数受限
- 由于事务提交时都要同步刷盘,则会导致大量的随机 I/O
因此更好的策略是 Steal + No Force:Page 可以被随时换入换出,也可以在任意时刻落盘,与事务脱钩。这样性能就可以大幅提升。
为了实现这一点,就需要额外的工作:
- 为了实现 Steal,需要 UNDO log:假如事务还未提交,其修改的值就已经落盘,此时发生 crash,在恢复后需要用 UNDO log 来回滚该执行了一半的事务。
- 为了实现 No Force,需要 REDO log:假如事务已经提交,但数据还未落盘,此时发生 crash,在恢复后需要用 REDO log 来重做未落盘的事务。
总结下来就是下图(来源):