对比 B+ Tree 文件组织 / LSM Tree 文件组织（第二篇：LSM Tree）

Posted on Edited on In

B+ Tree 与 LSM Tree 是现今各类数据库中使用的比较多的两种数据结构，它们都可以作为数据库的文件组织形式，用于以相对高效的形式来执行数据库的读写。

本文简述了这两种数据结构的操作方式与操作开销，并对比了其自身的优缺点。

LSM-Tree

LSM-Tree 最早是由 Patrick O'Neil 等人在 The Log-Structured Merge-Tree (LSM-Tree) 这篇论文中提出的，作者在论文中阐明：

由于传统的 B-Tree 类型的索引，其实时维护（插入、删除）开销很高。因此提出了 LSM-Tree 这种基于磁盘的数据结构，来为在较长时间内产生高速文件写入（或删除）的场景提供低成本的索引。

LSM-Tree 采用对写入进行延迟、批次化的算法，通过类似合并排序的高效方法，将更改以级联的方式从内存逐步推进到一个或多个磁盘组件中。

最初的 LSM-Tree

问题之源

当我们大量的采用 B-Tree 及其变体这类数据结构来存储索引、数据等的时候，我们能通过这类平衡树获得不错的读效率。从查找角度讲只需要 logN的时间复杂度；从存储角度讲，结合 Buffer Pool， 我们能做到通常一次查询最多只需要一次 Random I/O。（以上内容详情可见本系列文的第一篇）

但为了维持这种高效读取所产生的代价就是：复杂的更新与随之带来的缓慢的更新耗时。

我们知道，对 B-Tree 类型的数据结构进行更新操作时，除了查找 node 所需的时间外，还可能涉及到 node 的 merge、spilt、上下层移动等操作，这些操作通常都是 Random I/O。同时，这类更新操作都是是即时发生（in-place）的，即当场发生，当场完成，旧数据会被直接替换掉。

但我们早就已经知道一种最常用也是最简单的数据结构：日志（Log）。它结构非常简单，实现起来也容易，最重要的，由于对 log 文件的更新全部都是追加操作，是 Sequential I/O，对 HDD 磁盘结构很友好，写入速度会很快。

那么，我们能不能用 log 来替代 B-Tree 呢？如下的两个问题阻挡住了我们：

  1. 查询效率差：由于插入的随机性，我们想要查找的数据可能会存在于 log 文件中的任何位置上
  2. 空间利用率差：由于所有更新操作都是直接追加至 log 末尾，被更新的数据仍旧存在于更早的 log 中，我们需要采用非即时（out-of-place）的方式来将旧数据清理掉，但这种清理存在滞后性，这导致了空间利用率变差。

归并更新的日志树结构：LSM-Tree

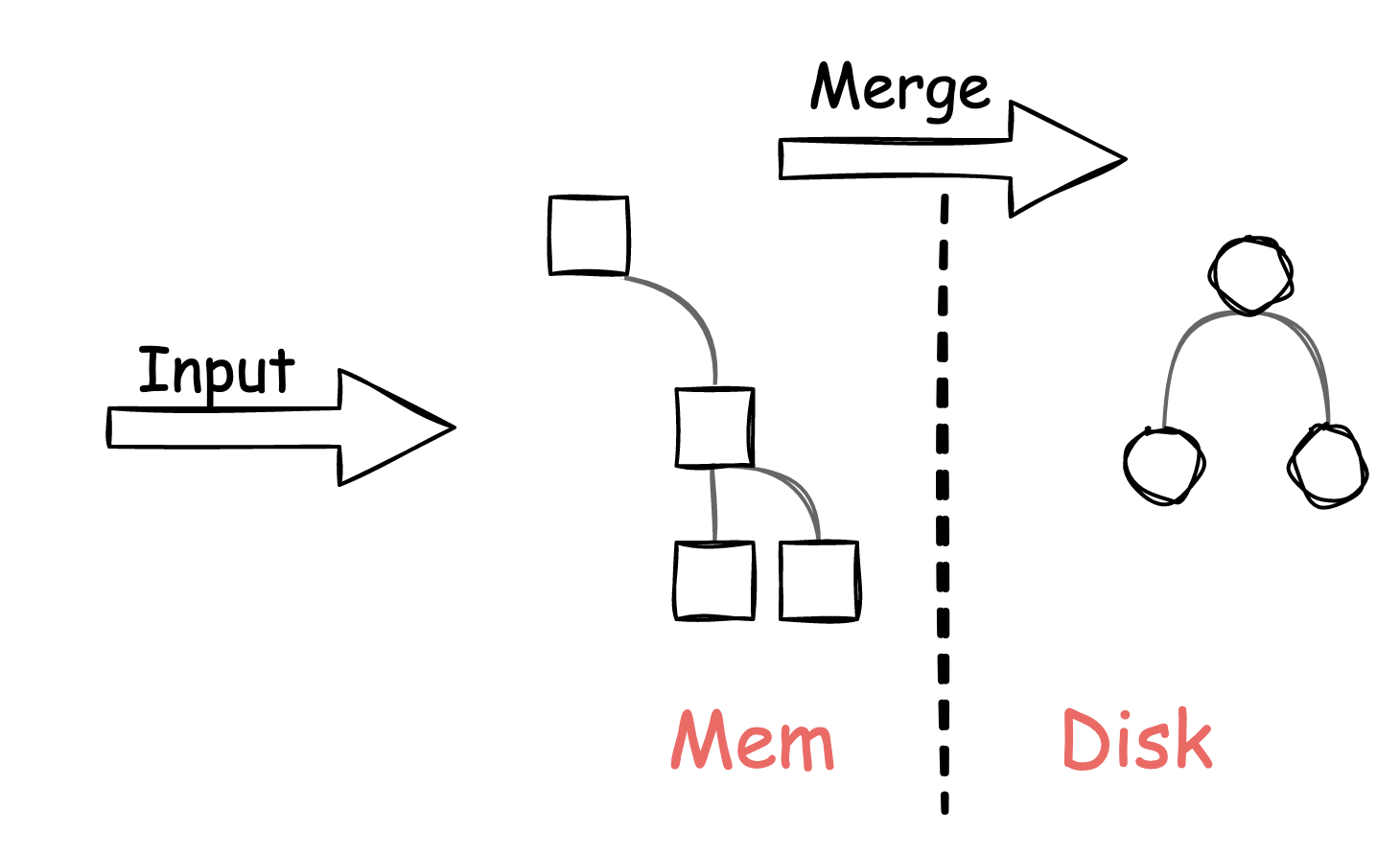
前述论文中首先假设了如下的一种数据结构（最基础的 LSM-Tree）：

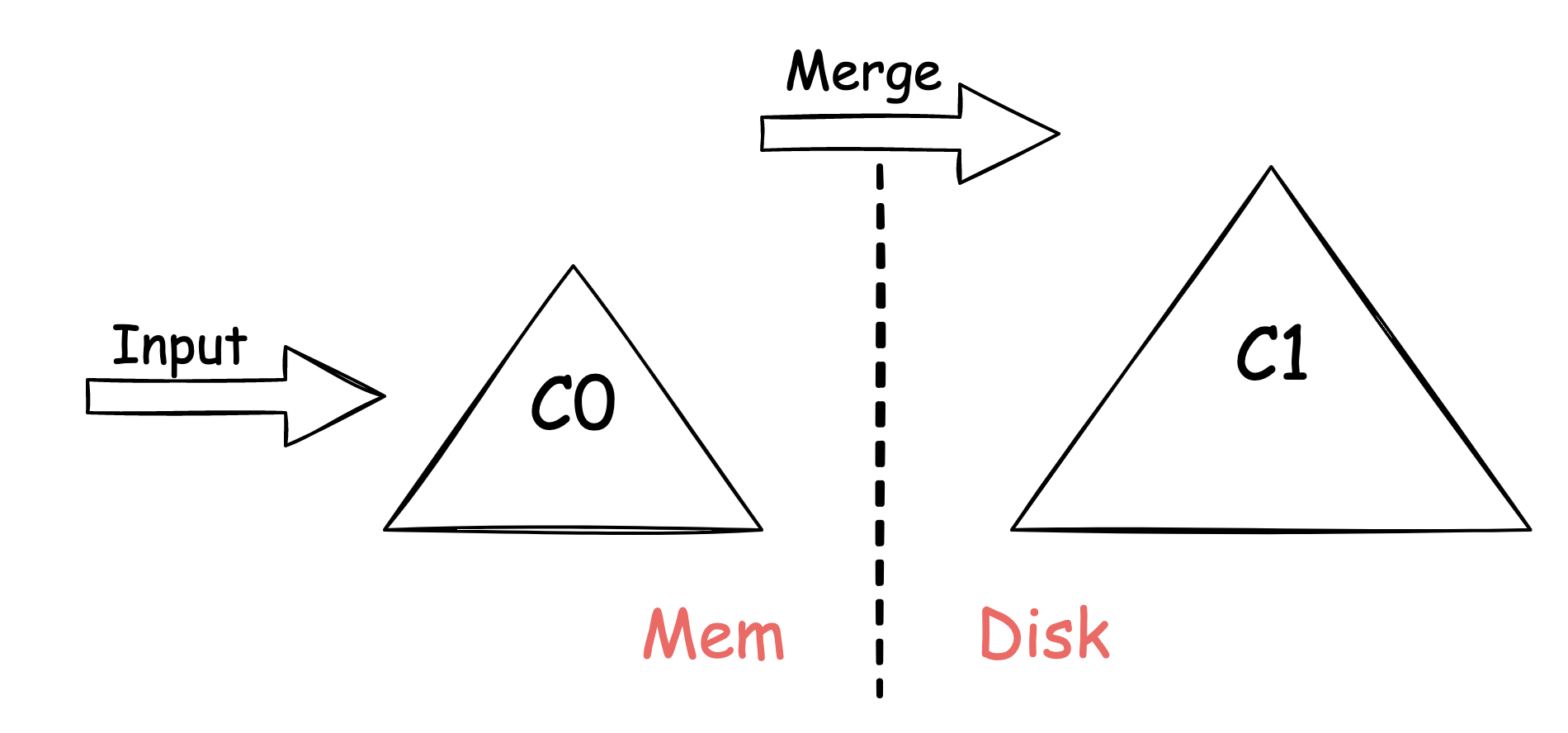
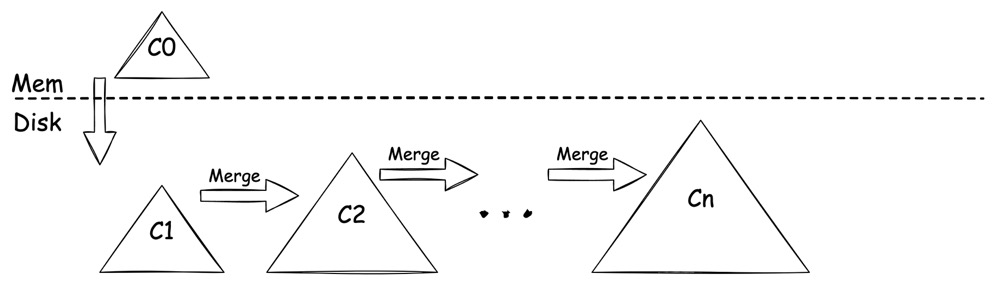
所有数据分成两个 Components 存放在 memory 和 disk 中，其中 memory 中的 Component 记为 \(C_0\)，disk 中的 Component 记为 \(C_1\)。\(C_0\) 相对\(C_1\)而言更小一些。

考虑到性能与可用性，一些常见的实践并没有在图上给出，如：

  • 仍然会通过 WAL 来进行恢复
  • \(C_1\) 仍然会采用 Buffer Pool 来提升读写性能

上述 LSM-Tree 在有数据写入时，新增数据首先写入到 \(C_0\)，之后会在一定时间的 delay 后，合并（merge）入 \(C_1\)。而在对数据查询时，会先在 \(C_0\)中查找，找不到再去 \(C_1\)。

在具体的 Component 内部，其数据结构采用了树形结构来存放：

  • \(C_0\) 作为存放在 memory 中的结构，不产生 I/O 消耗，不需要按 Page 或是 Batch 存取，因此采用了2-3-Tree 或 AVL-Tree 这类的平衡树。
  • \(C_1\) 作为存放在 disk 中的结构，仍旧采用了传统的 B-Tree 结构的变体（类似 SB-Tree），包括对顺序查询优化，单个节点可全满（100% full），页打包为多页块（multi-page block）来提升磁盘臂效率。

二阶（two components）LSM-Tree 的操作

插入

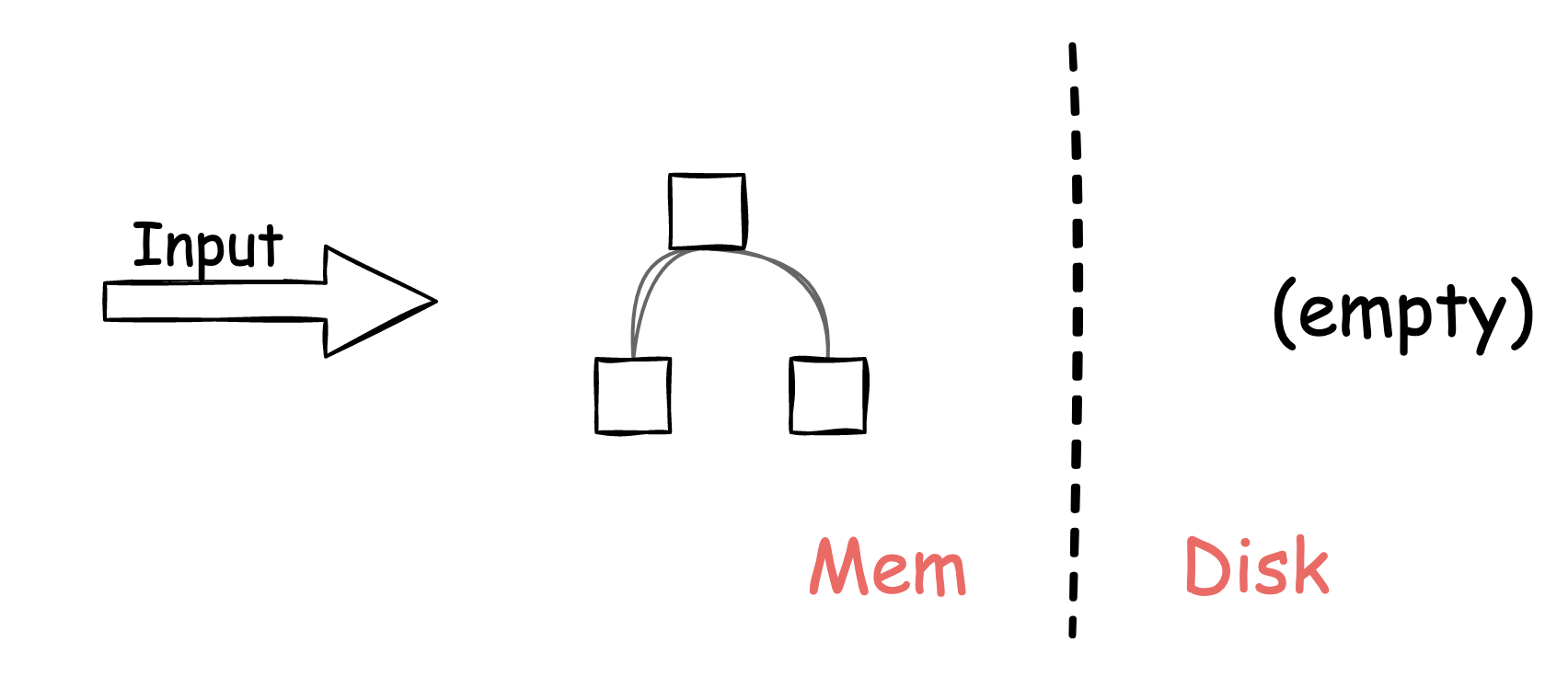
在整个数据结构最初的时候，并没有数据，因此刚开始的插入都只会影响 \(C_0\)，而不会影响\(C_1\)。如下图所示：

随着数据的不断增加，\(C_0\) 的容量达到了阈值：

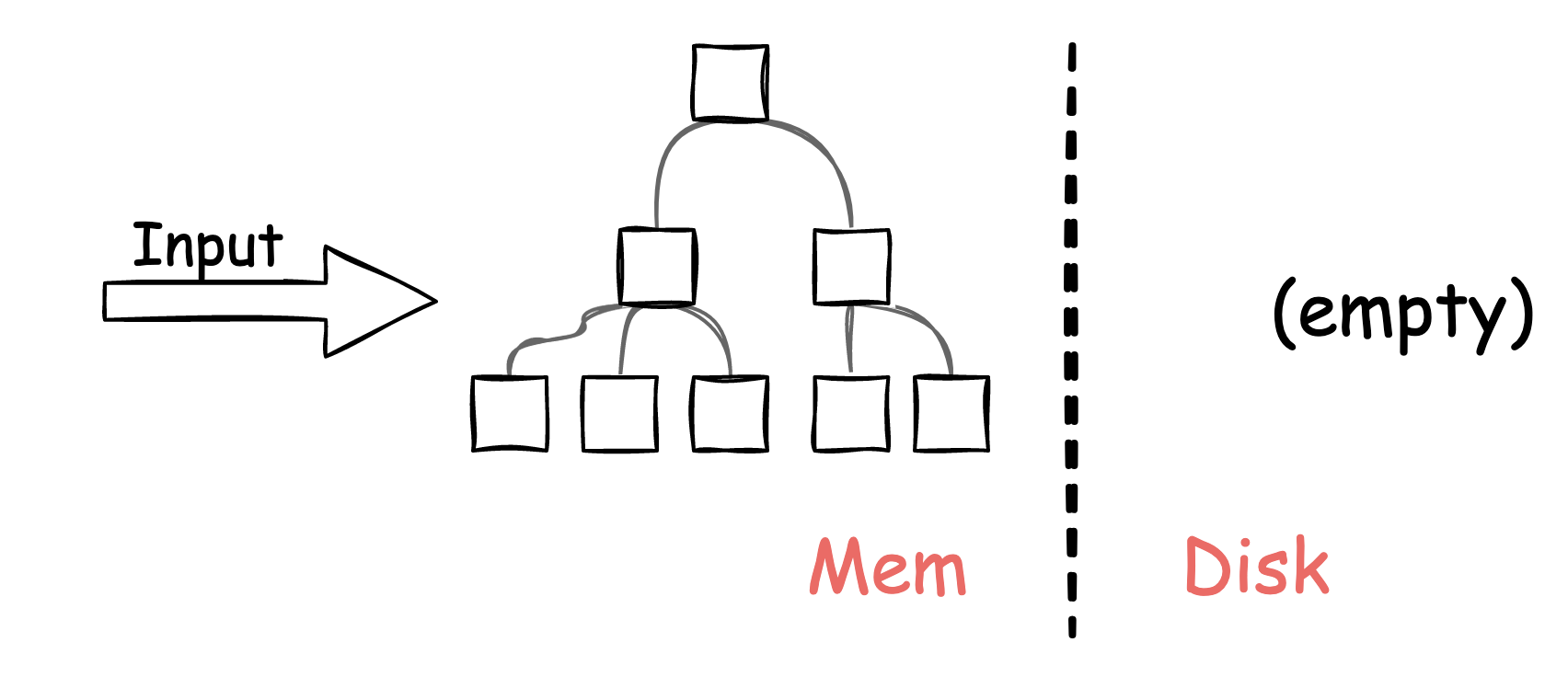
之后会开始第一次合并，从左侧树开始，合并一部分数据至 \(C_1\)。整个合并过程采用的是逐步合并的方式，一次合并只搬移一部分数据。

上图中对整个流程进行了一些简化，实际上从 \(C_0\) 移动的数据会先进入 Buffer Pool，最后由 Buffer Pool 选择何时写入 Disk

在经过了一段时间后，\(C_0\) 容量又一次触发阈值，需要将数据再次合并至 \(C_1\)：

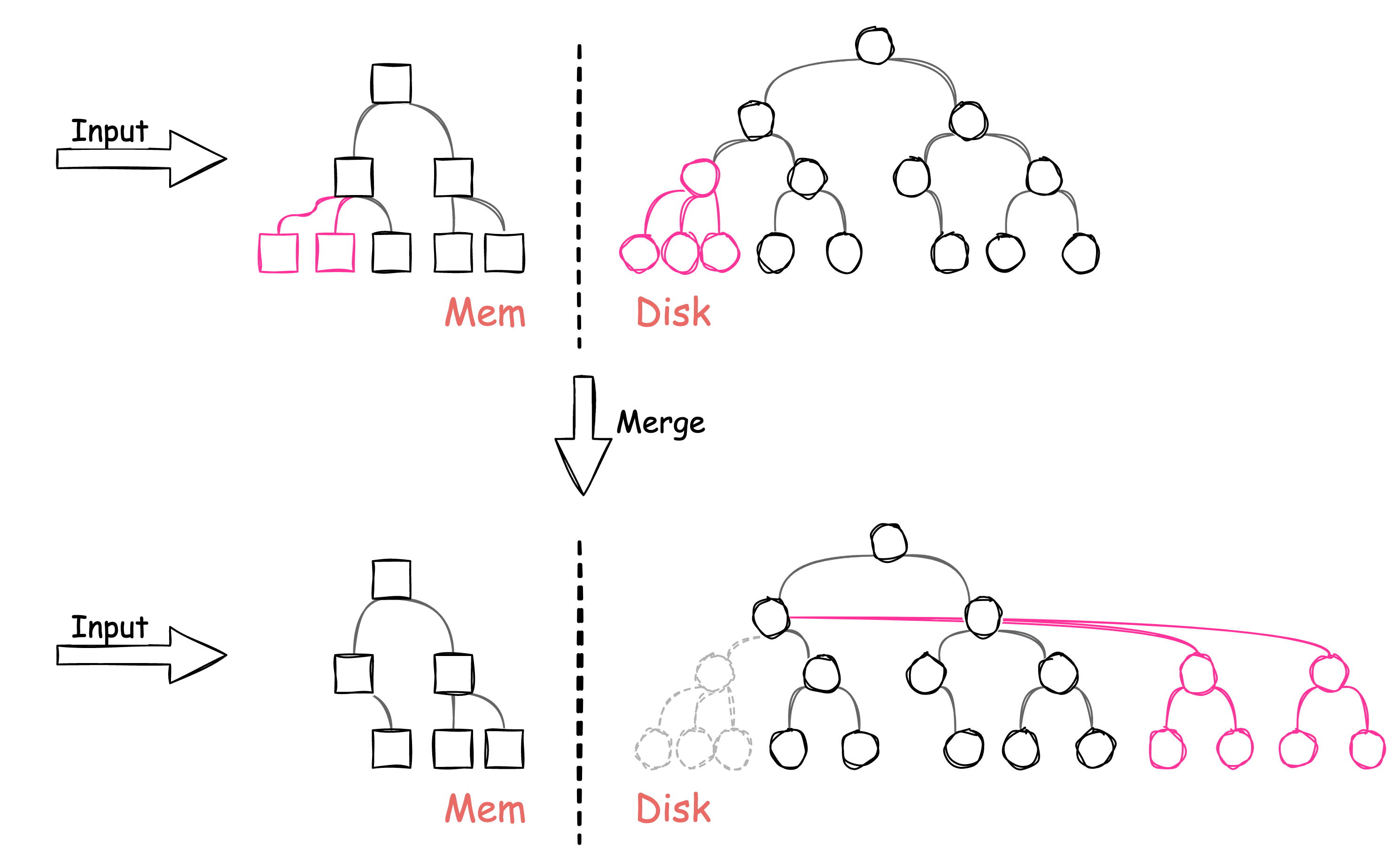
这里的关键之处在于，\(C_0\) 中被选择合并的部分已经移出，但在 \(C_1\) 中，合并后的新节点，直接追加在其尾部，而最左侧被合并的部分并没有被删掉，只是做了标记（虚线）。

正因为新节点直接追加，因此写入速度很快，而父节点中虽然需要更新指针，但因为 Buffer Pool 的存在，除了叶节点以外，其内部节点都可以保存在 Buffer Pool 中，更新它们也就没有 I/O 消耗。

在整个合并流程彻底完成后，\(C_1\)最左侧的冗余数据将会被异步的删掉。

之后随着数据不断的插入，合并不断的进行，\(C_1\) 中被合并的部分也不断的被选取为更右侧的树枝，这一过程称为滚动合并（rolling-merge）。

查找

查找操作从原理上讲就是先查找 \(C_0\)， 找不到就再查找 \(C_1\)。

通过观察我们能得知，最近插入的数据，其被访问的概率、频次会更高（LRU ）。正因为 \(C_0\) 存放的都是相对更新、距离插入时间更近的数据，因此\(C_0\) 能够有效的提升查询效率，从这个角度看，\(C_0\) 在查询中更像是一个缓冲区。

删除、更新

由于 LSM-Tree 这种结构，删除动作可以像插入一样高效：

先在 \(C_0\) 中查找被删除 entry 应该所在的位置，若\(C_0\) 中不存在这一 entry，那么插入一个删除标记（tombstone），若存在则替换。在之后的查找中，只要发现了该标记，就可认为对应的 entry 不存在。随着合并的进行，删除标记被合并至\(C_1\)，此时如果 \(C_1\) 中的确存在该 entry，那么将其删除即可。

而对于 LSM-Tree 结构下的更新操作，实际上与插入操作没有本质的区别。

n 阶 LSM-Tree

由于 LSM-Tree 这种结构同时使用到了 Memory 和 Disk，即 mem 资源与 I/O 资源。那么怎么样对 LSM-Tree 进行设计和调优，才能达到理论最佳呢？

论文中定义了一种指标：批次合并参数 M（The Batch-Merge Parameter M）。

全局上看，插入成本（insert cost）主要体现在滚动合并的过程中。因此定义 \(M\) 为滚动合并中，插入到 \(C_1\) 树的每个单页叶节点中的 \(C_0\) 树的平均 entreis 数量。即：

\(M = (S_p / S_e) \cdot (S_0/(S_0+S_1))\)

其中，

$S_e = $ 单个 entry 的 size（以 byte 计）

\(S_p=\) Page size（以 byte 计）

$S_0 = $ \(C_0\) 的 leaf level 的 size，（以 MByte 计）

$S_1 = $ \(C_1\) 的 leaf level 的 size，（以 MByte 计）

所以 \((S_p / S_e)\) 就是单页可存放的 entry 数量，\((S_0/(S_0+S_1)\) 是 \(C_0\) 中数据占总数据量的占比。

举例说明：

通常的实现中，\(S_1 = 40 \cdot S_0\)，\(S_p / S_e = 200\)， 因此 \(M = 5\)。

基于上述内容，我们可以知道，\(M\) 越大，平均合并的 \(C_0\) entry 越多，效率就越高。而假如 \(C_1\) 远大于 \(C_0\) 或者单个 entry 巨大导致单个页只能存放少量的几个 entries，那么就会导致 \(M\) 很小，甚至可能产生 \(M < 1\) 的情况。

怎么在成本最低的情况下让 \(M\) 达到最大

前面讲到， \(C_1\) 与 \(C_1\) 的大小差距越悬殊，\(M\) 会越小，所以我们就期望能在资源允许的情况下，尽可能的增大 \(C_0\)，来增大 \(M\)。

从成本角度看，整个 LSM-Tree 的成本包括：

  • 内存空间成本
  • 磁盘 I/O 成本

为了找到最小成本点，我们首先选取一个很大的 \(C_0\)，这种情况下，I/O 速率会相对较低。之后我们逐步的缩小 \(C_0\)，用昂贵的内存空间换取便宜的磁盘空间。一直到 I/O 速率达到全速状态。在这之后如果继续减少 \(C_0\) 的容量，就会导致 I/O 延迟加大。

实际上，即使是按照上述方式所选取出的 \(C_0\) 容量，如果在数据量稍大的场景下，也是十分庞大的，这就会导致内存投入过于昂贵。

扩展至 n 阶

从性能、成本的定性分析上我们知道，考虑到成本的限制，二阶的 LSM-Tree 其 \(C_0\) 和 \(C_1\) 之间的容量差距还是太大了，那么一种缓解的办法就是在 \(C_0\) 和 \(C_1\) 之间插入更多的中间层。

这样每一层的部分都与二阶一样，不断的向下一层合并。最终合并到最后一层。

此外，在论文给出的定理 3.1中证明了：每一层之间的容量比例为固定值时，整体滚动合并所产生的 I/O 速率（最小化速率等同于最小化 I/O 成本）最小。（相关证明可见论文 3.4 节）

现代 LSM-Tree 实现

Patrick O'Neil 等人的论文通过提出 LSM-Tree，开创性的解决了 log 结构存在的问题。但看一看如今的各种数据库中对 LSM-Tree 的实现，似乎都没有采用文中所提到的滚动合并的办法。其原因主要在于实现起来太过复杂。

但 LSM-Tree 本身的 memory + disk 存储的结构、以追加文件的方式提升写性能、证明层级之间保持比例一致等等概念与原则已经影响到了后续所有的 LSM-Tree 实现与改进。

数据结构与合并策略

从前文可知，在最初提出的 LSM-Tree 的滚动合并策略中，其 Disk Component 会不断地被更新，因此这种处理方式会增加并发控制与故障恢复的复杂度。

因此在现代的实现中，数据结构大都采用如下的实现：

  • Mem Component：使用并发安全的数据结构如 skiplist、B+Tree 等
  • Disk Component：B+Tree 或 SSTable（Sorted String Table），其中 SSTable 使用的会更多
    • SSTable 通常包含两部分，data block 和 index block，分别用于顺序存放 k-v pair 与对 pair 进行索引
    • Disk Component 通常是不可变的，因此只可以新增或删除，不允许修改（简化并发控制）

合并

正因为随着各种操作的不断实施，Component 的内容会不断增多，因此需要采用循序渐进的合并，来消除重复数据，减少数据总量。

前面已经讲到，为了降低并发控制和故障恢复的成本，现代的 LSM-Tree 其 disk component 都被限制为不可变，那么也就无法使用最初论文中提到的滚动合并。因此有了如下两种合并策略：

1. Leveling

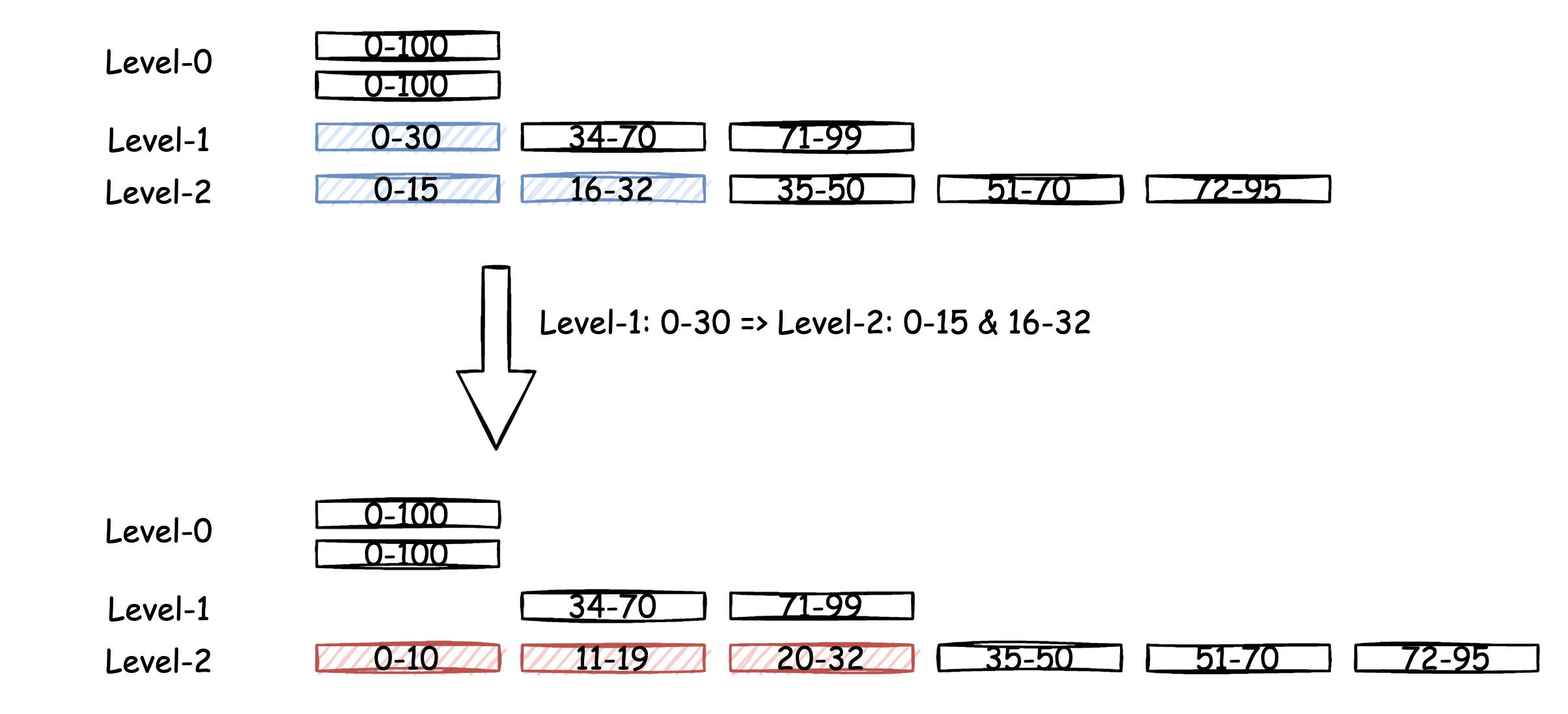
leveling 策略下，与最初的 disk component 类似，每一层（level）只存在一个 component，它不可修改，只能在容量达到阈值时向下合并。

其中，\(Level_{L}\) 的容量是 \(Level_{L-1}\) 的 \(T\) 倍，因此 \(Level_{L}\) 层的 component 将会被来自 \(Level_{L-1}\) 层的 component 合并数次，直到其容量达到 \(Level_{L}\) 层的最大阈值。

就如同上图中所示，其中 component 上的标注表示了当前 component 中存放 key 的 range。\(Level_0\) 尝试向 \(Level_1\) 合并，合并后，\(Level_1\) 变大，但还未达到其阈值，因此不再向 \(Level_2\) 合并。

2. Tiering

tiering 策略下，每一层都可能存在最多 \(T\) 个 components，一旦 components 的数量达到 \(T\) ，那么这 \(T\) 个 component 将会一并合入下一层。同样的，每一个 component 都不可变。

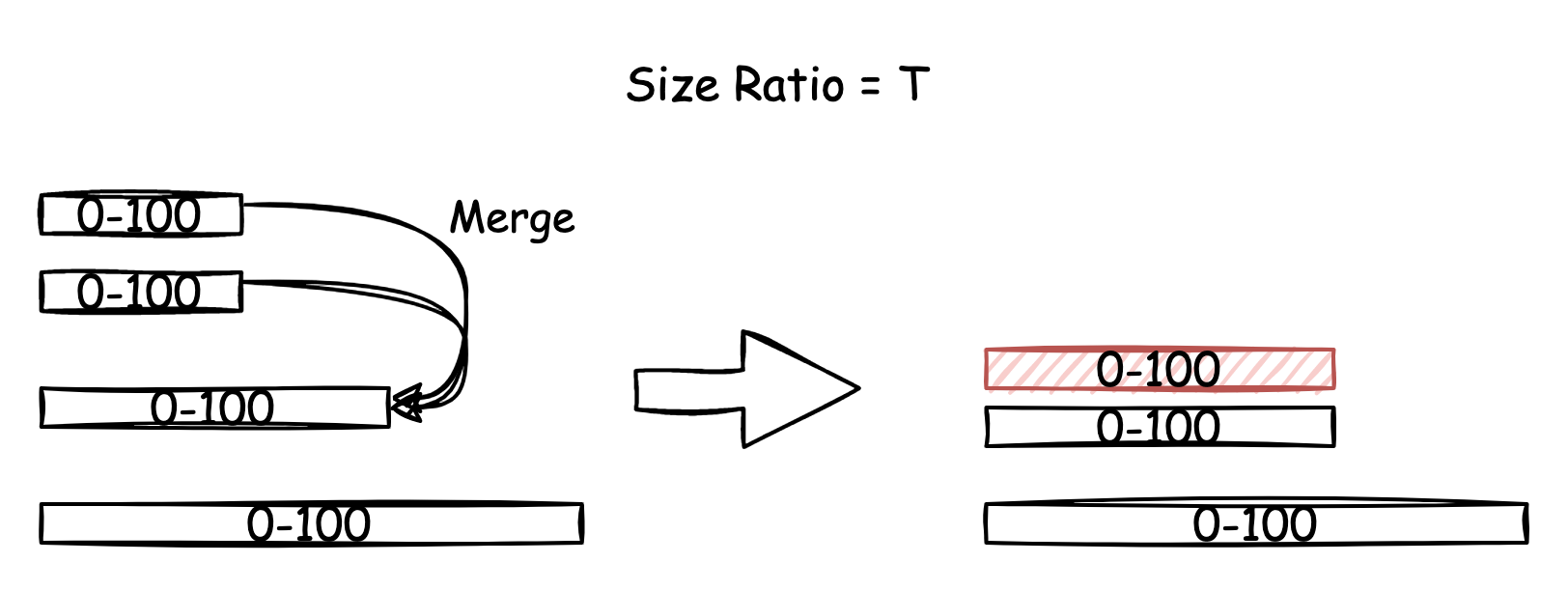
如上图所示，\(Level_0\) 的 component 数量达到了最大阈值，因此共同合并成为 \(Level_1\) 的新的一个 component。

优化方案

通过前面的描述，我们或许会发现一些问题：

  • 即使存在 Mem Component，但对于冷数据的查询，仍然需要从 Disk Component 中查找，对于一个 n 层的 LSM-Tree，最坏情况下要 n 次随机 IO（查找的 key 不存在时的情况也一样）
  • 如果不只是用作 index 结构，而是直接作为存放数据的结构，数据量会大很多，那么在合并时就可能产生很多问题，比如反复在 memory 与 disk 之间交换数据、阻塞正常操作请求等

基于以上的问题，常见的优化方案有：

Bloom Filter

通过布隆过滤器，我们能够用极其少的空间消耗，来表明 key 的不存在性（可以确保不存在，但无法确保存在）。

其主要思想是通过 n 不同的 hash 函数计算同一个输入，得到 n 个位置点，当有查找需求时，如果待查找的 key 通过这 n 个 hash 函数后并没有得到相同的 n 个位置点，那么就能证明该 key 一定不存在与当前数据结构中，反之则不一定。

我们知道布隆过滤器不存在假阴性（false negative），但会存在假阳性（false positive），对于其假阳性的概率有如下公式计算：

\((1-e^{-kn/m})^k\)

其中，\(k\) 是 hash 函数的数量，\(n\) 是 key 的数量，\(m\) 是 bit-slot 的数量。

所以对满足最小假阳性的参数，有：

\(k = \frac mnln2\)

在实际当中多数系统采用了 \(10\ bit/key\) 的设置，那么代入公式后就能得出这种设置的假阳性率仅为 1% 。

由于布隆过滤器非常小的空间占用，以及高效的查询效率，他能极大地提升查询性能。

Partitioning

前面提到了，随着层数的增加，Component 逐渐变大导致合并变得低效与缓慢。

分区正是这样一种优化，它讲大的 Component 分解为数个小的部分，这样一来：

  • 可以限制合并操作对空间、时间的要求。最早 LSM-Tree 实际上就通过滚动合并实现了对合并数据的限制，分区可以看做是对滚动合并的简化
  • 每一个分区都可以设置特定的 key range，那么我们就可以仅对具有 key 重叠的分区进行合并，这对一些顺序插入或偏斜更新（skewed update）的场景很有用。
    • 由于不存在重叠，顺序插入甚至不需要合并，只要将足够大的分区向下层移动；
    • 而对于偏斜更新，不涉及到更新范围的 “冷分区”，其合并的频次也非常低。

leveling 策略下的 partition 方案，是将单个 Component 拆分成多个固定大小的 SSTable，每一个 SSTable 都标记了自己所存储的 key range。

由于 \(Level_0\) 的产生是由 mem component 直接复制得到，因此比较特殊，没有分 key range，其余 \(Level\) 都按 key range 进行分区。

在进行合并时，选择需要合并 \(Level_i\) 的 partition（选择策略可以是任意算法，如 round robin），之后选择 \(Level_{i+1}\) 的所有被 key range 覆盖到的 partition，合并后产生 \(Level_{i+1}\) 新的 SSTable。

对于 tiering 策略的 partitioning，可参见 LSM-based Storage Techniques: A Survey。

LevelDB 的实现

Google 在其 BigTable 的论文当中，描述了 BigTable 这种分布式结构化数据存储系统，其 Tablet Server 的存储结构正式采用了 LSM-Tree 来实现。但文中并没有详细的讲述设计细节。

在这之后，Google 的 Sanjay Ghemawat 和 Jeff Dean 两位计算机科学家，共同编写并开源了一个单机版的 k-v 数据库 LevelDB，其设计思想与 BigTable 中所提到的存储设计十分相似。这给了外界对其 LSM-Tree 实现一窥究竟的机会。

LevelDB 用 C++ 编写，代码量不大，实现清晰、简洁。其 API 也十分简单：

  • Put(key,value)
  • Get(key)
  • Delete(key)

存储架构

LevelDB 的整体存储架构如下图所示：

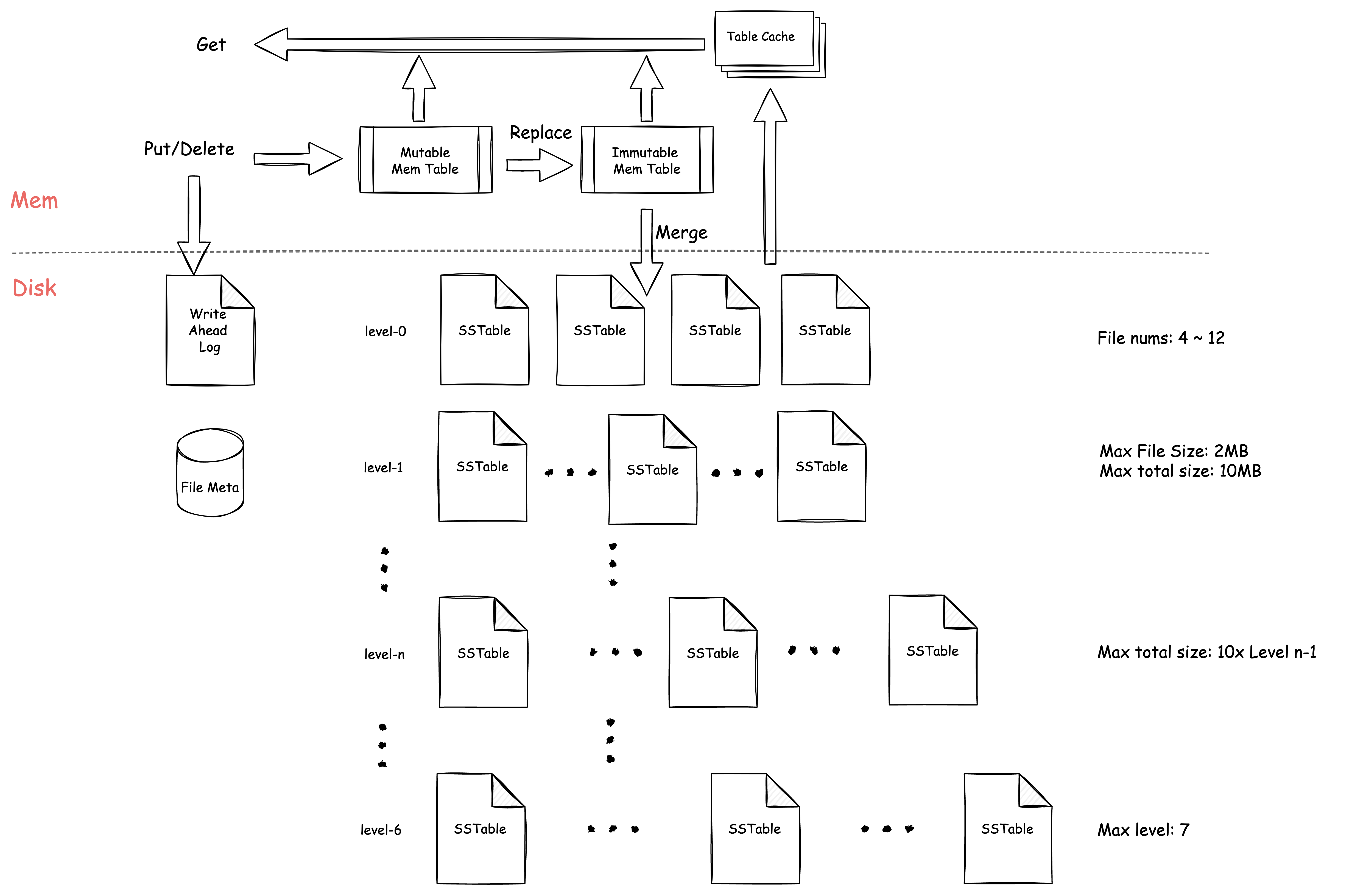
如上图所示，整个架构中，主要由 MemTable、ImmutableMemTable、TableCache、SSTable、WAL、FileMeta 这几种组件构成。

通常写的动作会同时进入 WAL 与 MemTable。而后续的 MemTable -> ImmutableMemTable -> SSTable 的过程，都会在后台线程中完成。

读操作会在 MemTable、ImmutableMemTable、TableCache 中进行，其中 TableCache 可以看做是缓存层，当未命中时会在磁盘文件中继续查找。

对于 SSTable 的结构，单个文件最大 2MB。\(Level_0\) 由于是从内存中直接转换而来，比较特殊，默认 4 个文件，超出后就开始尝试合并（Compaction），最多不能超过 12 个文件。

\(Level_1\) 的层最大容量限制是 10MB，从 \(Level_1\) 开始，每增加一层，其最大容量是上一层的 10 倍。

最大层数默认是 7 层。

根据上述我们就能简单的计算出：\(Level_6\) 的最大容量是 \(10 * 10^5 = 1000000 MB = 1 TB\) ，而所有层都达到最大的情况下，其空间利用率（数据量/实际存储量）约为 90%。

Log、MemTable 与 SST

下文的所有数据结构，都包含了一个基础的数据结构：Slice。

Slice 可以存放任何类型的数据，唯一的不同是，Slice 的定义：

1
2
3
4
5
6
7
8
class Slice {
  public:
    ... ...
  
  private:
    const char* data_;
    size_t size_;
}

可见除了数据本身以外，还包含了数据长度信息。

之后的数据结构中，所提到的 “数据”，都指的是 Slice。

Log File Format

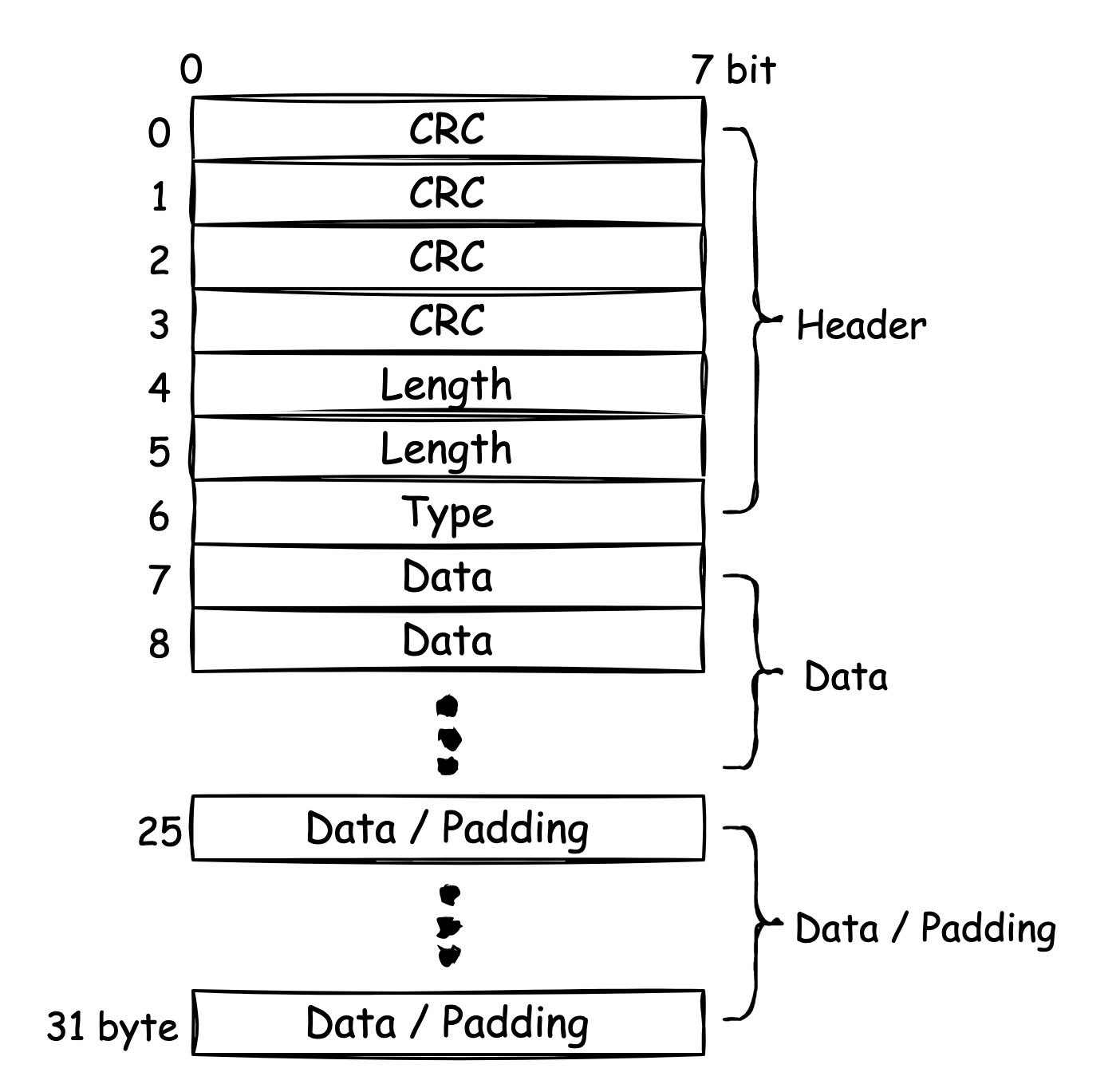
如上图所示，Log file 是由一个又一个 log-block 构成，每一个 block 的 size 为 32 KB （最后一个 block 除外）。

每个 block 都包含一个 7 byte 的 header，其中前 4 byte 存放该 block 中数据的 CRC，第 5、6 byte 存放数据长度，第 7 byte 存放数据类型。

其类型包括如下：

  • kFullType：待插入的数据长度小于当前 block 剩余空间，可以直接完整的插入
  • kFirstType：待插入数据长度大于当前 block 剩余空间，且当前 block 放置的是待插入数据的第一部分
  • kMiddleType：待插入数据长度大于当前 block 剩余空间，且当前 block 放置的是待插入数据的中间部分
  • kLastType：待插入数据长度小于当前 block 剩余空间，但当前 block 放置的是待插入数据的最后一部分

此外，图中的 padding，是因为若当前 block 剩余空间小于 header 的 7 bytes，则直接进行 padding。

MemTable

MemTable 由于是内存中的数据结构，因此其对具体的空间占用要求并不严格，见如下定义：

1
2
3
4
5
6
7
8
9
class MemTable {
  public:
   ... ...
  private:
    KeyComparator comparator_;
    int refs_;
    Arena arena_;
    SkipList<const char*, KeyComparator> table_;
}

显然，MemTable 实际上是用跳表来存储数据的。从插入、查找效率上讲，跳表与红黑树区别不大，但实现更简单。

properties：

  • comparator_是当前 MemTable 中 key 的比较器
  • refs_ 是引用计数，用于并发控制
  • arena_ 跳表实际使用的内存空间
  • table_跳表的引用
SSTable

SSTable 的全称是 Sorted String Table，因此顾名思义，这种文件结构中存储的是有序的 Strings。

下图描述了 SSTable 的文件结构：

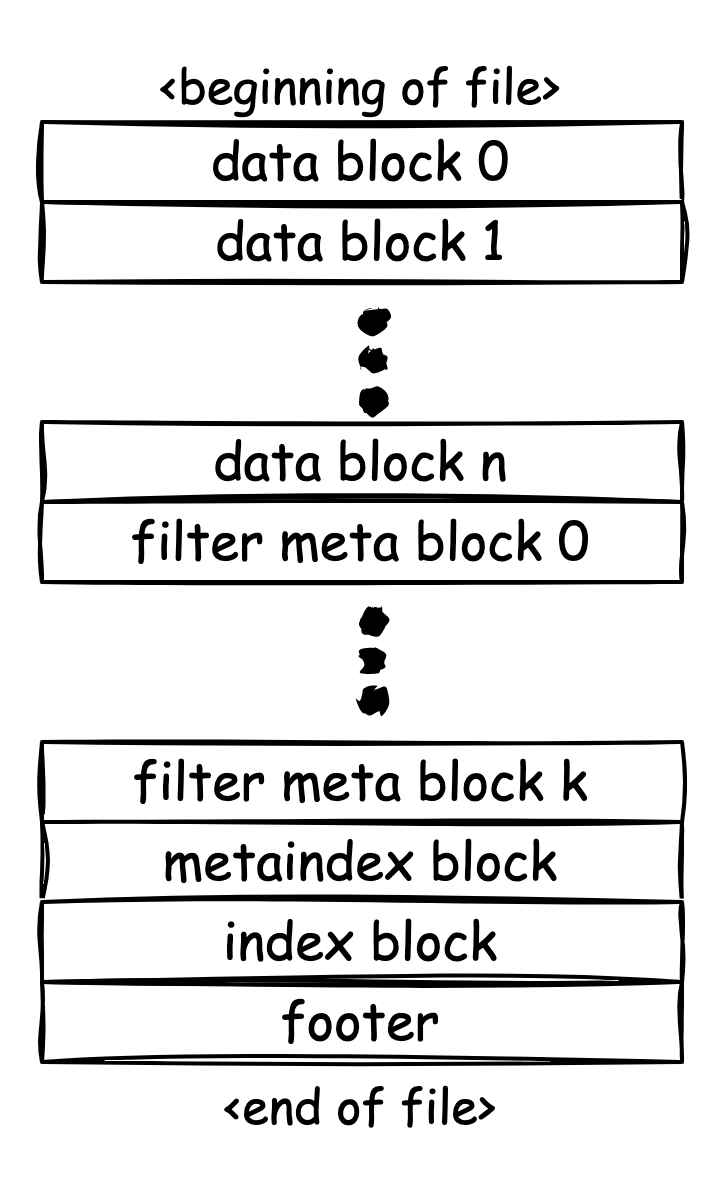
SST 的默认大小是2 MB。可以看到 SST 中除了 Footer 以外，主要存放的就是各种类型的 Block。Block 可以理解为一次磁盘操作所传输的数据量，类似于 Page，默认是 4 KB。

对于 Block，有如下结构：

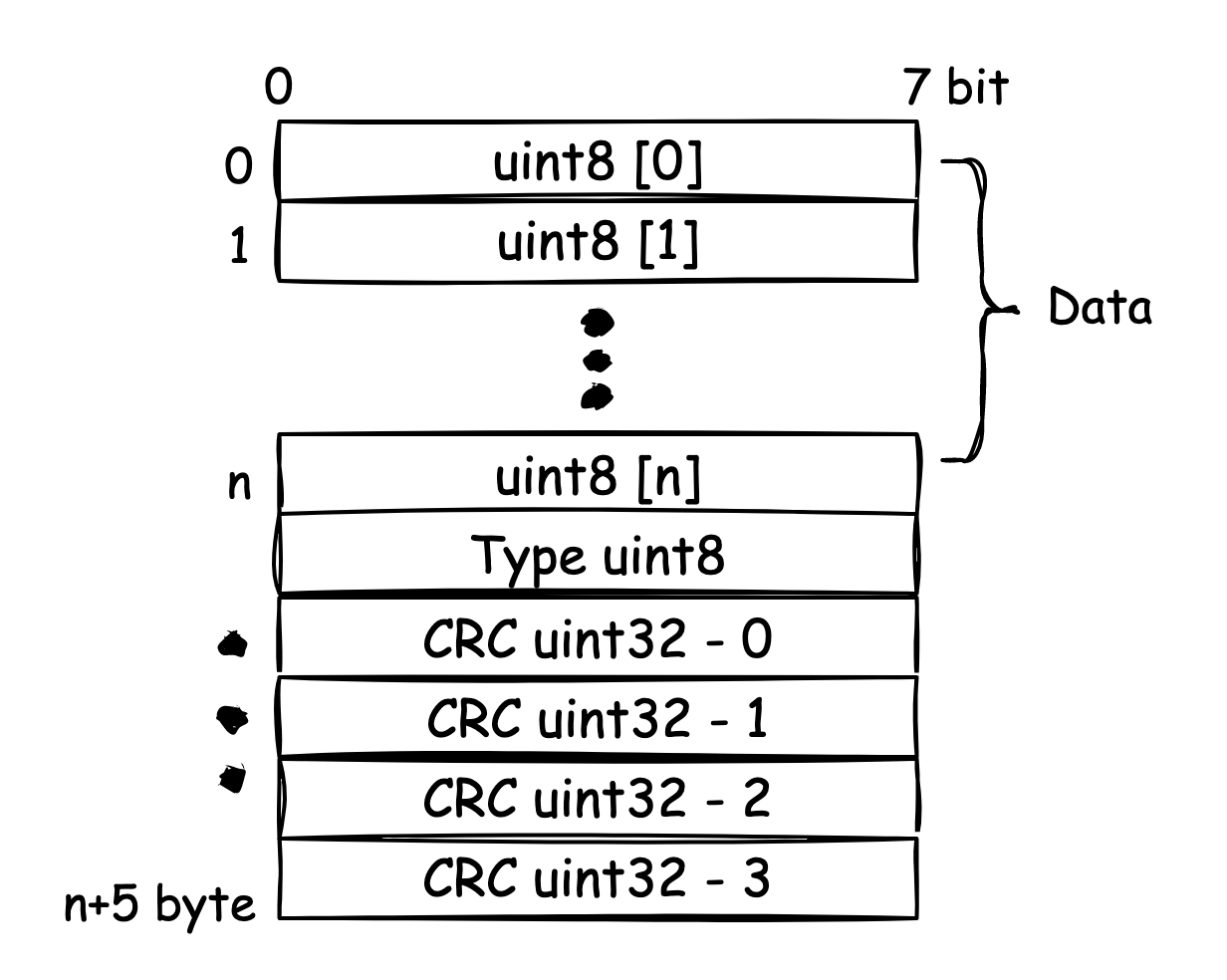
其结构相对简单，除了数据以外，就是 type 与 CRC，而 type 目前只有是/否压缩两种状态。

对于SST中的各种组成部分：

  • DataBlock 中按顺序放置了实际的数据

  • FilterMetaBlock 中放置的是各种 filter，如最常见的 Bloom Filter，也可以放置其他用户自定义的 filter

  • MetaIndexBlock 只有单个 block，其中放置的是各种 filter 数据的具体起始位置

  • IndexBlock 中存放了每一个 key 的大小与位置，以 BlockHandle 结构来表示，其中 BlockHandle：

    •   class BlockHandle {
    public:
     ... ...
    private:
      uint64_t offset_;
      uint64_t size_;
  }

  • Footer 中也存放了两个 BlockHandle 结构，分别指示了 MetaIndex 与 Index block 的 size 与在文件中的 offset 信息

写入操作

在实际写入之前，首先会判断当前写入空间是否足够，若不足则需要等待。大致的流程见下图：

我们能看到，假如 MemTable(mem) 空间不足，会判断是否已经存在 ImmutableMemTable(imm)，如果不存在，会把当前 mem 转换为 imm，并创建一个新的 mem 用于本次以及后续的写入。此时会同步触发后台的 Compaction，因此 imm 主要用于延迟从 memory 到 disk 的合并，提升写入速度。

那么很显然，如果在 MemTable(mem) 空间不足的同时，imm 也存在，就代表当前已经有 Compaction 进行中，所以需要等待。

读取操作

读取操作虽然在代码实现上内容不少（涉及到多种查找动作），但原理上相对简单：

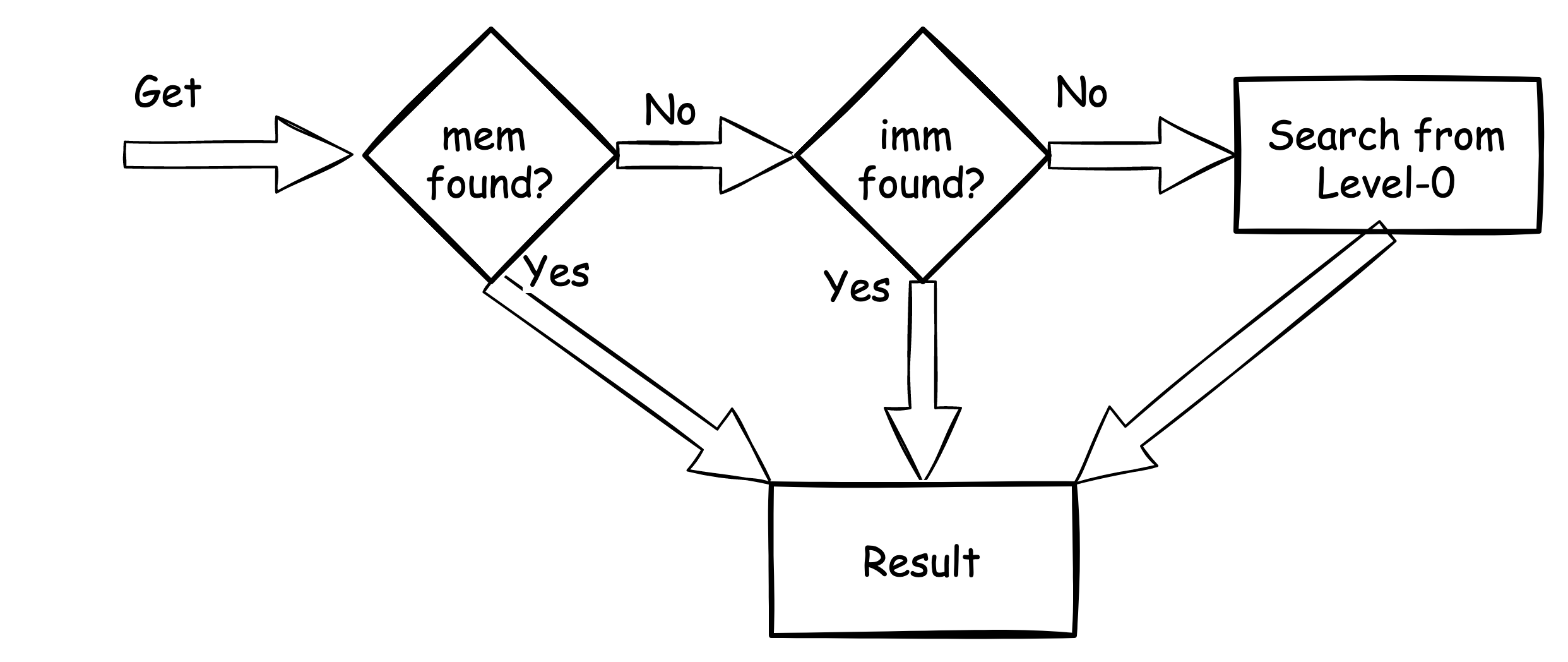
先在 mem 查找，找不到就到 imm 查找，再找不到就需要去 SST 中查找 （这里隐藏了 TableCache 作为缓存层的实现细节）。

Compaction

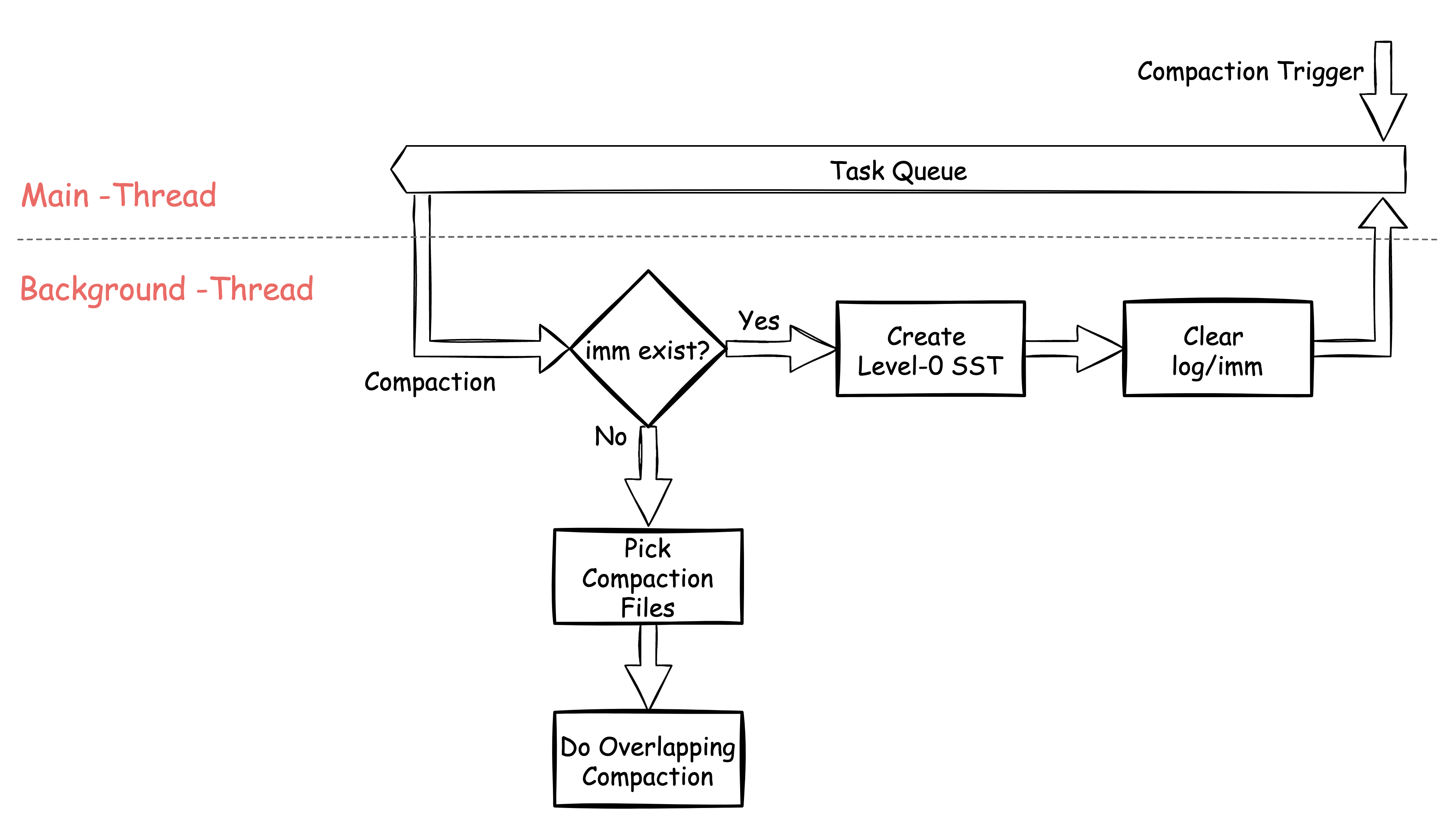
Compaction 的动作，是独立的在一个后台线程中进行的，但每一次 Compact，都是由各种逻辑主动触发。

Compaction 线程通过一个 queue 来获取任务，而这个 “任务”，其实就是执行 Compaction 的函数指针和参数。在没有任务要执行时，后台线程处于 Wait 状态。

根据前文的配置限定，在某一层的总容量超出阈值时，就会从左至右依次选择一个 SST 准备向下合并。

这里的 \(Level_0\) 层会与其他不同， \(Level_0\) 的数据都来自 ImmutableMemTable，因此会先将 imm 的数据生成一个 \(Level_0\) 层的 SST，之后由于已经落盘，之前 WAL 中与 imm 有关的 log 不再需要了，因此将之删除。在执行完成 \(Level_0\) 的 Compaction 后，后台线程会再发送一个触发 Compaction 的任务回到任务队列。

假如 Compaction 发现不存在 imm 则正常进行其他 \(Level\) 的合并工作：

  1. 寻找合适的 \(Level\) ，寻找标准就是总容量是否超出阈值
  2. 按顺序（round robin）选取待合并 \(Level_n\) 的一个 SST，同时根据 overlap 的情况选取 \(Level_{n+1}\) 中的数个文件，准备进行合并
  3. 若不存在 overlap，那么就可以简单的将这个 SST 挪到下一层即可完成，这种情况称作 TrivialMove
  4. 否则，将 SST 中的数据根据 range 的实际情况，与\(Level_{n+1}\) 中的 SST 进行合并即可，过程中可能涉及到创建新的 SST
  5. 最后删除无用的文件，完成 Compaction

Reference

  1. The Log-Structured Merge-Tree (LSM-Tree)
  2. LSM-based Storage Techniques: A Survey
  3. LevelDB Source